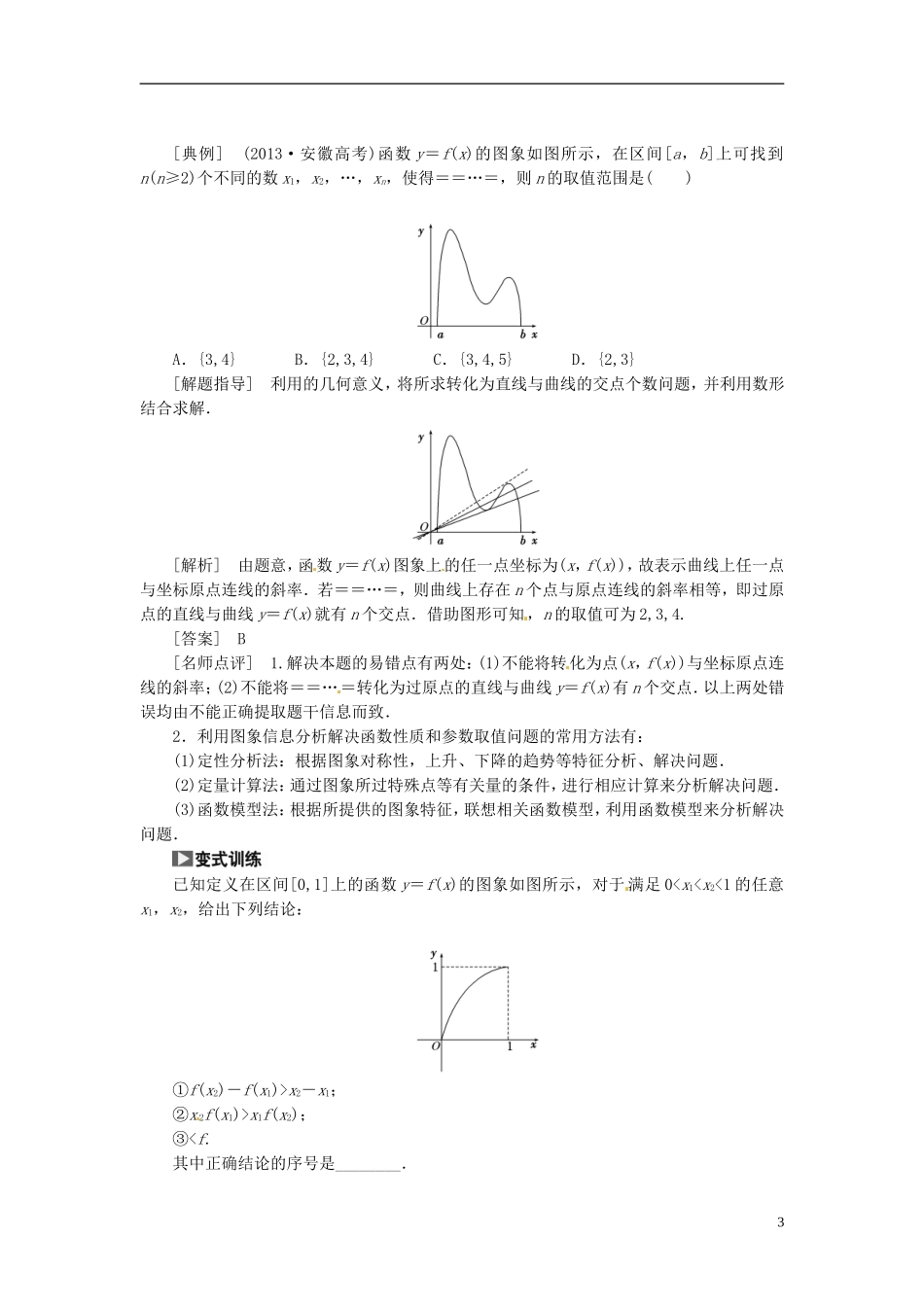
【考纲下载】1.在实际情境中,会根据不同的需要选择图象法、列表法、解析法表示函数.2.会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式解的问题.1.利用描点法作函数图象基本步骤是列表、描点、连线.首先:①确定函数的定义域;②化简函数解析式;③讨论函数的性质(奇偶性、单调性、周期性、对称性等).其次:列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等),描点,连线.2.利用图象变换法作函数的图象(1)平移变换:y=f(x)――→y=f ( x - a ) ;y=f(x)――→y=f ( x ) + b .(2)伸缩变换:y=f(x)――→y=f ( ωx ) ;y=f(x)――→y=Af ( x ) . (3)对称变换:y=f(x)――→y=- f ( x ) ;y=f(x)――→y=f ( - x ) ;y=f(x)――→y=- f ( - x ) . (4)翻折变换:y=f(x)――→y=f (| x |) ;y=f(x)――→y=| f ( x )| .1.函数 y=f(x)的图象关于原点对称与函数 y=f(x)与 y=-f(-x)的图象关于原点对称一致吗?提示:不一致,前者是本身的对称,而后者是两个函数图象间的对称.2.一个函数的图象关于 y 轴对称与两个函数的图象关于 y 轴对称有何区别?提示:函数 y=f(x)的图象关于 y 轴对称是自身对称,说明该函数为偶函数;而函数 y=f(x)与函数 y=f(-x)的图象关于 y 轴对称,是两个函数的图象对称.3.若函数 y=f(x)的图象关于点(a,0)(a>0)对称,那么其图象如何变换才能使它变为奇函数?其解析式变为什么?提示:向左平移 a 个单位即可;解析式变为 y=f(x+a).11.函数 y=x|x|的图象经描点确定后的形状大致是( )解析:选 A y=x|x|=为奇函数,奇函数图象关于原点对称.2.(2013·福建高考)函数 f(x)=ln(x2+1)的图象大致是( )解析:选 A 函数 f(x)=ln(x2+1)的定义域为(-∞,+∞),又因为 f(-x)=f(x),故f(x)为偶函数且 f(0)=ln 1=0,综上选 A.3.(2013·北京高考)函数 f(x)的图象向右平移 1 个单位长度,所得图象与曲线 y=ex关于 y 轴对称,则 f(x)=( ) A.ex+1 B.ex-1 C.e -x+1 D.e-x-1解析:选 D 与曲线 y=ex关于 y 轴对称的曲线为 y=e-x,函数 y=e-x的图象向左平移 1个单位长度即可得到函数 f(x)的图象,即 f(x)=e-(x+1)=e-x-1.4.函数 y=f(x)在 x∈[-2,2]的图象如图所示,则当 x∈[-2,2]时,f(x)+f(-x)=________...