高三数学空间角与距离习题精选精讲VIP免费

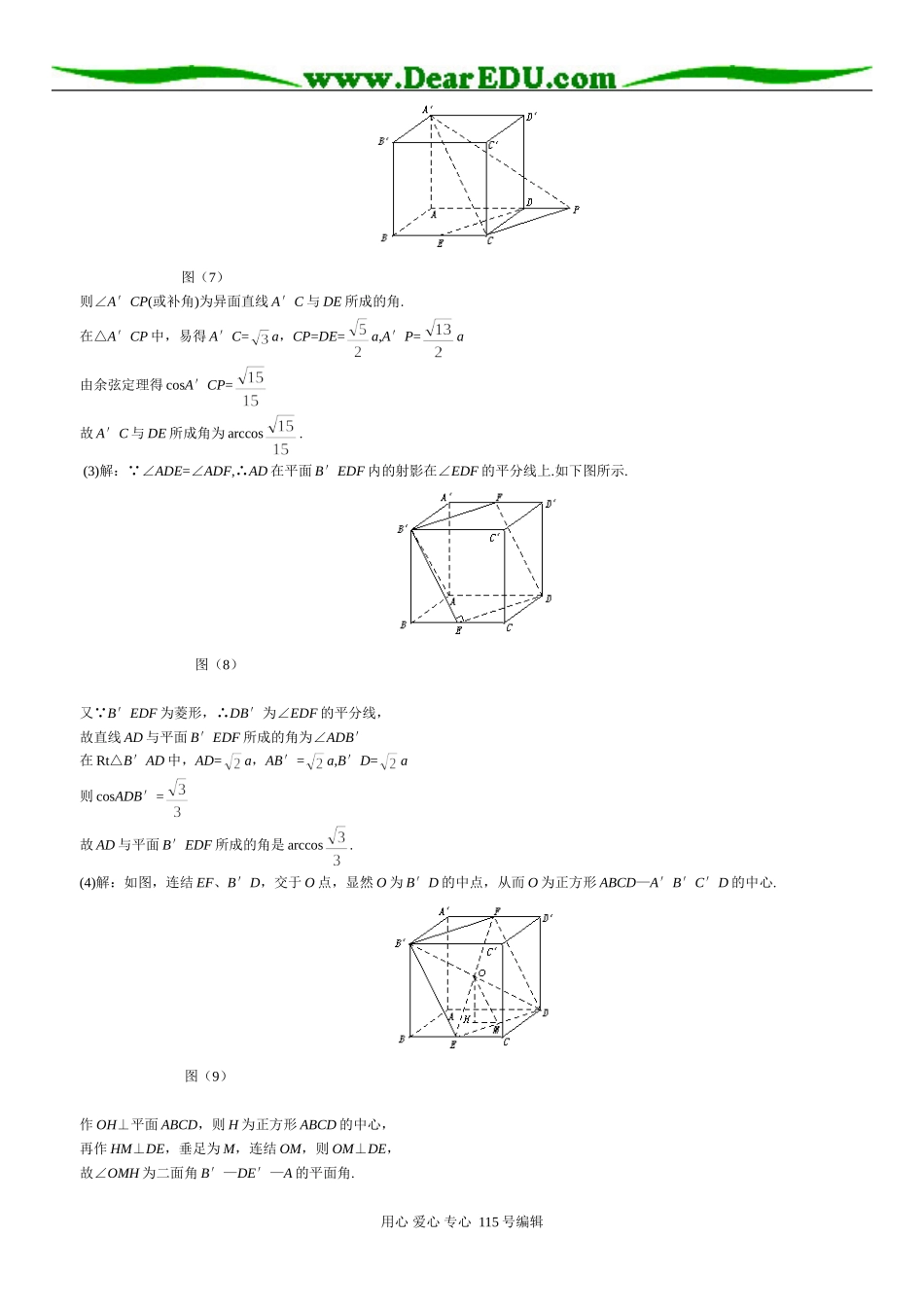
空间角与距离（1）异面直线所成的角——空间角的最小元素直线与直线所成角是立体几何的所成角（线线角、线面角、面面角）中最简单的一种，只需要把两条直线（或其中一条直线）平移，使它们相交于一点，就可以把两条异面直线所成角的问题转变为平面中两条相交直线所夹角的问题了.要注意的是角的取值范围，分清那个角是这两条直线的所成角（或者它的补角）.其范围是.【例1】如图（1）所示，在空间四边形ABCD中，已知AD=1，BC=，且AD⊥BC，对角线BD=，求AC和BD所成的角.图（1）【分析】作平行线，找与异面直线所成的角相等的平面角，将空角问题转化为平面问题.【解析1】如图（2）所示，分别取AD、CD、AB、BD的中点E、F、G、H，连结EF、FH、HG、GE、GF.由三角形中位线定理知，EF∥AC，且EF=，GE∥BD，且GE=.GE和EF所成的锐角（或直角）就是AC和BD所成的角.同理，GH=，GH∥AD，HF∥BC.又AD⊥BC，∴.∴在△EFG中，图（2）∴，即AC和BD所成的角为.【解析2】如图（3），在平面BCD内，过C作CE∥BD，且CE=BD，连DE，则DE∥BC且DE=BC.∴∠ACE就是AC和BD所成的角（若∠ACE为钝角，则∠ACE的补角就是AC和BD所成的角）.又AD⊥BC,∴AD⊥DE.∴图（3）在△ACE中，∴∠ACE=90°，即AC和BD所成的角为90°.【点评】求异面直线所成的角常采用“平移线段法”.平移的方法一般有下面三种类型：利用图有已有的平行线平移；利用特殊点（线段的端点或中点）作平行线平移；补形平移，计算异面直线所成的角通常放在三角形中进行.（2）线面角——直线与射影的夹角为主体直线与平面所成的角分两种，一是平面的斜线与平面所成的锐角，即斜线与平面内的射影所夹的角；二是平面的垂线与平面所成的直角.直线与平面所成角不存在补角的问题.直线与平面成角的范围是.【例2】如图（4），在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．(Ⅰ)求证：OD∥平面PAB；(Ⅱ)当k＝时，求直线PA与平面PBC所成角的大小.【解析】(Ⅰ) O、D分别为AC、PC的中点：用心爱心专心115号编辑∴OD∥PA,又AC平面PAB,图（4）∴OD∥平面PAB.(Ⅱ) AB⊥BC,OA=OC,∴OA=OC=OB,又 OP⊥平面ABC,∴PA=PB=PC.取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC∴∠ODF是OD与平面PBC所成的角.又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.图（5）在Rt△ODF中,sin∠ODF=,∴PA与平面PBC所成角为arcsin【点评】求直线与平面所成的角常利用射影转化为相交直线所成的角.（3）二面角——用平面角来量度面面成角是立体几何中的所成角问题的重点，二面角的两个面是两个半平面，因此二面角中有钝角存在，二面角的取值范围与线线角、线面角不同，它的取值范围是.二面角的大小往往转化为其平面角的大小，从而又化归为三角形的内角大小求解，以利用平面几何、三角函数等重要知识.【例3】在棱长为a的正方体ABCD—A′B′C′D′中，E、F分别是BC、A′D′的中点.图（6）(1)求证：四边形B′EDF是菱形；(2)求直线A′C与DE所成的角；(3)求直线AD与平面B′EDF所成的角；(4)求面B′EDF与面ABCD所成的角.【解析】(1)证明：如上图所示，由勾股定理，得B′E=ED=DF=FB′=a,下证B′、E、D、F四点共面，取AD中点G，连结A′G、EG，由EGABA′B′知，B′EGA′是平行四边形.∴B′E∥A′G,又A′FDG,∴A′GDF为平行四边形.∴A′G∥FD，∴B′、E、D、F四点共面故四边形B′EDF是菱形.(2)解：如图（7）所示，在平面ABCD内，过C作CP∥DE，交直线AD于P，用心爱心专心115号编辑图（7）则∠A′CP(或补角)为异面直线A′C与DE所成的角.在△A′CP中，易得A′C=a，CP=DE=a,A′P=a由余弦定理得cosA′CP=故A′C与DE所成角为arccos.(3)解： ∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上.如下图所示.图（8）又 B′EDF为菱形，∴DB′为∠EDF的平分线，故直线AD与平面B′EDF所成的角为∠ADB′在Rt△B′AD中，AD=a，AB′=a,B′D=a则cosADB′=故AD与平面B′EDF所成的角是arccos.(4)解：如图，连结EF、B′D，交于O点，显然O为B′D的中点，从而O为正方形ABCD—A′B′C′D的中心.图（9）作OH⊥平面ABCD，则H为正方形ABCD的中心，再作HM⊥DE，垂足为M...