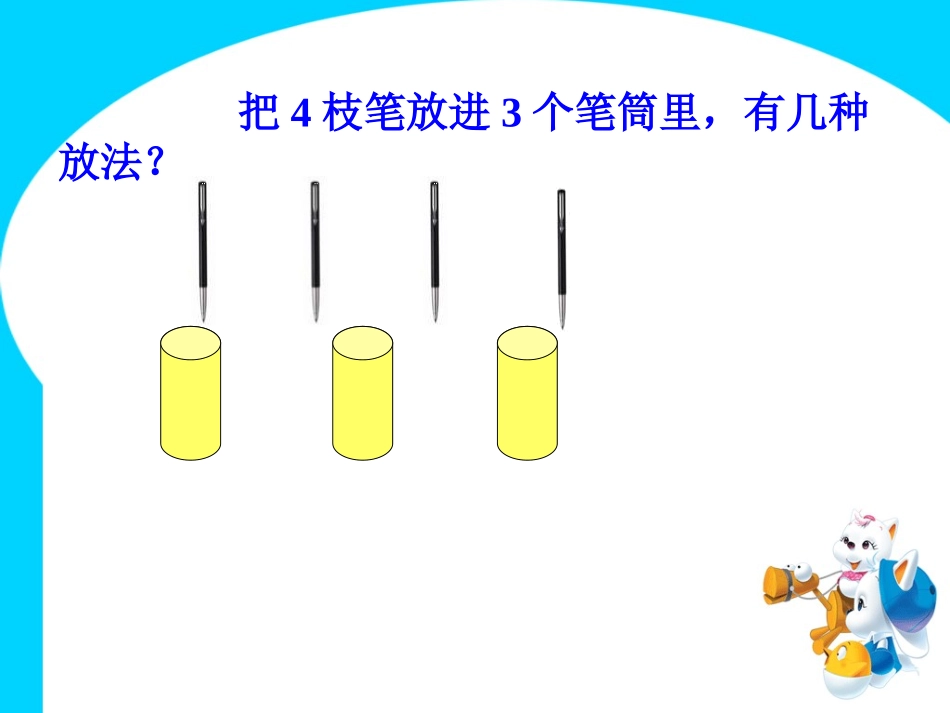
灵宝市第三小学有三本书,放入两个抽屉里,有几种方法?试试看。方法一方法二把4枝笔放进3个笔筒里,有几种放法?总有一个笔筒里,至少放进2枝笔。把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,这是为什么?我们从最不利的原则去考虑:如果我们先让每个笔筒里放1枝笔,最多放3枝。剩下的1枝还要放进其中的一个笔筒。所以不管怎么放,总有一个笔筒里至少放进2枝笔。假如一个鸽舍里飞进一只鸽子,5个鸽舍最多飞进5只鸽子,还剩下2只鸽子。所以,无论怎么飞,至少有2只鸽子要飞进同一个笼子里。7只鸽子飞回5个鸽舍,至少有2只鸽子要飞进同一个鸽舍里,为什么?把5本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进3本书。这是为什么?5÷2=2……1把7本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进多少本书?为什么?7÷2=3……1把9本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进多少本书?为什么?9÷2=4……18÷3=2……28只鸽子飞回3个鸽舍,至少有()只鸽子要飞进同一个鸽舍。为什么?3我们先让一个鸽舍里飞进2只鸽子,3个鸽舍最多可飞进6只鸽子,还剩下2只鸽子,无论怎么飞,所以至少有3只鸽子要飞进同一个笼子里。至少数=商数+1计算绝招“抽屉原理”又称“鸽巢原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。“抽屉原理”在数论、集合论、组合论中都得到了广泛的应用。“抽屉原理”又称“鸽巢原理”,最先是由19世纪的德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。“抽屉原理”在数论、集合论、组合论中都得到了广泛的应用。狄利克雷(1805~1859)综合应用:1、34个小朋友要进4间屋子,至少有()个小朋友要进同一间屋子。2、13个同学坐5张椅子,至少有()个同学坐在同一张椅子上。3、新兵训练,战士小王6枪命中了43环,战士小王总有一枪至少打中()环。4、咱们班上有58个同学,至少有()人在同一个月出生。5、从街上人群中任意找来20个人,可以确定,至少有()个人属相相同。5599338822从扑克牌中取出两张王牌,在剩下的52张扑克牌任意抽牌。(1)从中抽出18张牌,至少有几张是同花色?18÷4=4(张)……2(张)4+1=5(张)答:至少有5张是同花色。20÷13=1(张)……7(张)1+1=2(张)答:至少有2张数字相同。(2)从中抽出20张牌,至少有几张数字相同?例3:盒子里有同样大小的红球和蓝球各4个。要想摸出的球一定有2个同色的,最少要摸出几个球?31.把红、黄、蓝三种颜色的球各10个放到一个袋子里,要保证取到两个颜色相同的球,至少取()个球。42.王东玩掷骰子游戏,要保证掷出的骰子总数至少有两次相同,他最少应掷()次。73.把红、黄、蓝三种颜色的球各10个放到一个袋子里,要保证取到三个颜色相同的球,至少取()个球。7箱子里有5种不同品牌的果冻各20粒,要想保证摸到同品牌的果冻4粒,最少要摸出多少粒果冻?