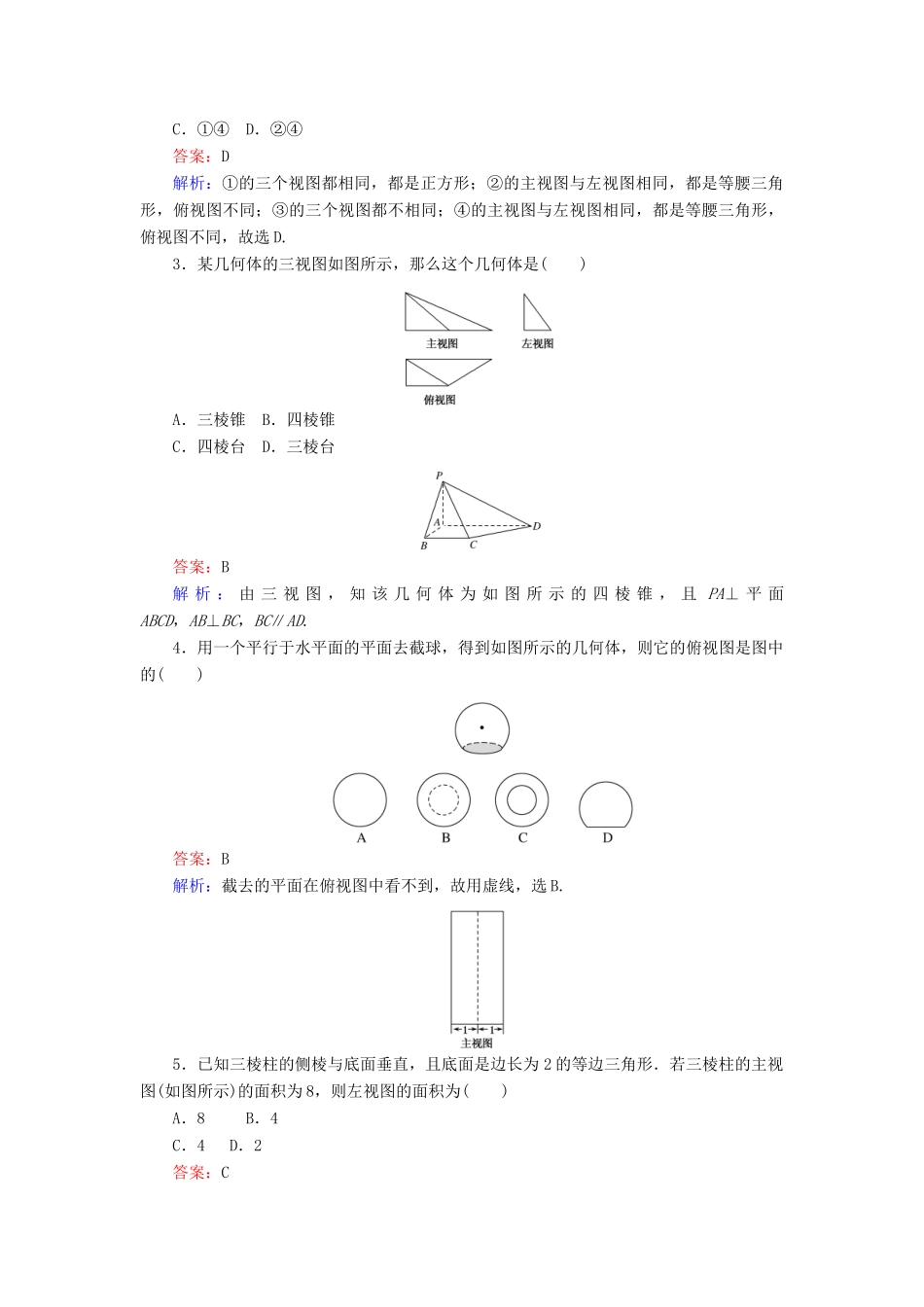
第7课时1.1.5三视图课时目标1.掌握三视图的基本原理,能画出简单空间图形(长方体、球、圆柱、圆锥等的简易组合)的三视图,并能识别上述的三视图所表示的立体模型.2.掌握简单几何体的三视图,直观图之间的相互转化.识记强化三视图(1)选取三个两两互相垂直的平面作为投射面,其中一个投射面水平放置,叫做水平投射面,投射到这个平面内的图形叫做俯视图.(2)一个投射面放置在正前方,这个投射面叫做直立投射面,投射到这个平面内的图形叫做主视图.(3)和直立、水平两个投射面都垂直的投射面叫做侧立投射面,通常把这个平面放在直立投射面的右面,投射到这个平面内的图形叫做左视图.课时作业一、选择题(每个5分,共30分)1.下列说法正确的是()A.任何几何体的三视图都与其摆放的位置有关B.任何几何体的三视图都与其摆放的位置无关C.有的几何体的三视图与其摆放的位置无关D.正方体的三视图一定是三个全等的正方形答案:C解析:球的三视图与其摆放位置无关,正方体的三视图不一定是三个全等的正方形.2.下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.②③C.①④D.②④答案:D解析:①的三个视图都相同,都是正方形;②的主视图与左视图相同,都是等腰三角形,俯视图不同;③的三个视图都不相同;④的主视图与左视图相同,都是等腰三角形,俯视图不同,故选D.3.某几何体的三视图如图所示,那么这个几何体是()A.三棱锥B.四棱锥C.四棱台D.三棱台答案:B解析:由三视图,知该几何体为如图所示的四棱锥,且PA⊥平面ABCD,AB⊥BC,BC∥AD.4.用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是图中的()答案:B解析:截去的平面在俯视图中看不到,故用虚线,选B.5.已知三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形.若三棱柱的主视图(如图所示)的面积为8,则左视图的面积为()A.8B.4C.4D.2答案:C解析:设该三棱柱的侧棱长为a,则2a=8,所以a=4.该三棱柱的左视图是一个矩形,一边长为4,另一边长等于三棱柱底面等边三角形的高,为,所以左视图的面积为4.故选C.6.已知正三棱锥V-ABC的主视图、俯视图如图所示,其中VA=4,AC=2,则该三棱锥的左视图的面积为()A.9B.6C.3D.答案:B解析:由三视图与原几何体之间的关系可知此几何体的左视图为一个等腰三角形,且此等腰三角形的底边长等于原几何体的底面边长,两腰的长度不等于原几何体的侧棱长,其高的长度等于原几何体的高.由所给数据易解得原几何体的高为2,所以左视图的面积为S=×2×2=6,故选B.二、填空题(每个5分,共15分)7.如图所示,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为________.答案:1解析:三棱锥P-ABC的主视图与左视图为等底等高的三角形,故它们的面积相等,面积比值为1.8.已知一正四面体的俯视图如图所示,它是边长为2cm的正方形,则这个正四面体的主视图的面积为________cm2.答案:2解析:构造一个边长为2cm的正方体ABCD-A1B1C1D1,在此正方体中作出一个符合题意的正四面体A-B1CD1,易得该正四面体的主视图是一个底边长为2cm,高为2cm的等腰三角形,从而可得主视图的面积为2cm2.9.如图是一个空间几何体的三视图,则该几何体为__________.答案:正六棱台解析:注意俯视图的“定位”作用,结合主、左视图将其还原.三、解答题10.(12分)根据三视图(如图所示),画出物体的实物草图.解:由三视图,知物体的上部分是一个圆柱,下部分是一个底面边长相等的长方体,且圆柱的下底面圆内切于长方体的上底面正方形.实物草图如图所示.11.(13分)(1)如图是截去一角的长方体,画出它的三视图.(2)如图,螺栓是棱柱和圆柱的组合体,画出它的三视图.解:(1)该图形的三视图如图所示.(2)螺栓的三视图如图所示.能力提升12.(5分)如图用□表示一个立方体,用表示两个立方体叠加,用表示三个立方体叠加,那么右图中有7个正方体叠成的几何体,正视图是()答案:B13.(15分)用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它至少需要多少个小立方块?最多...