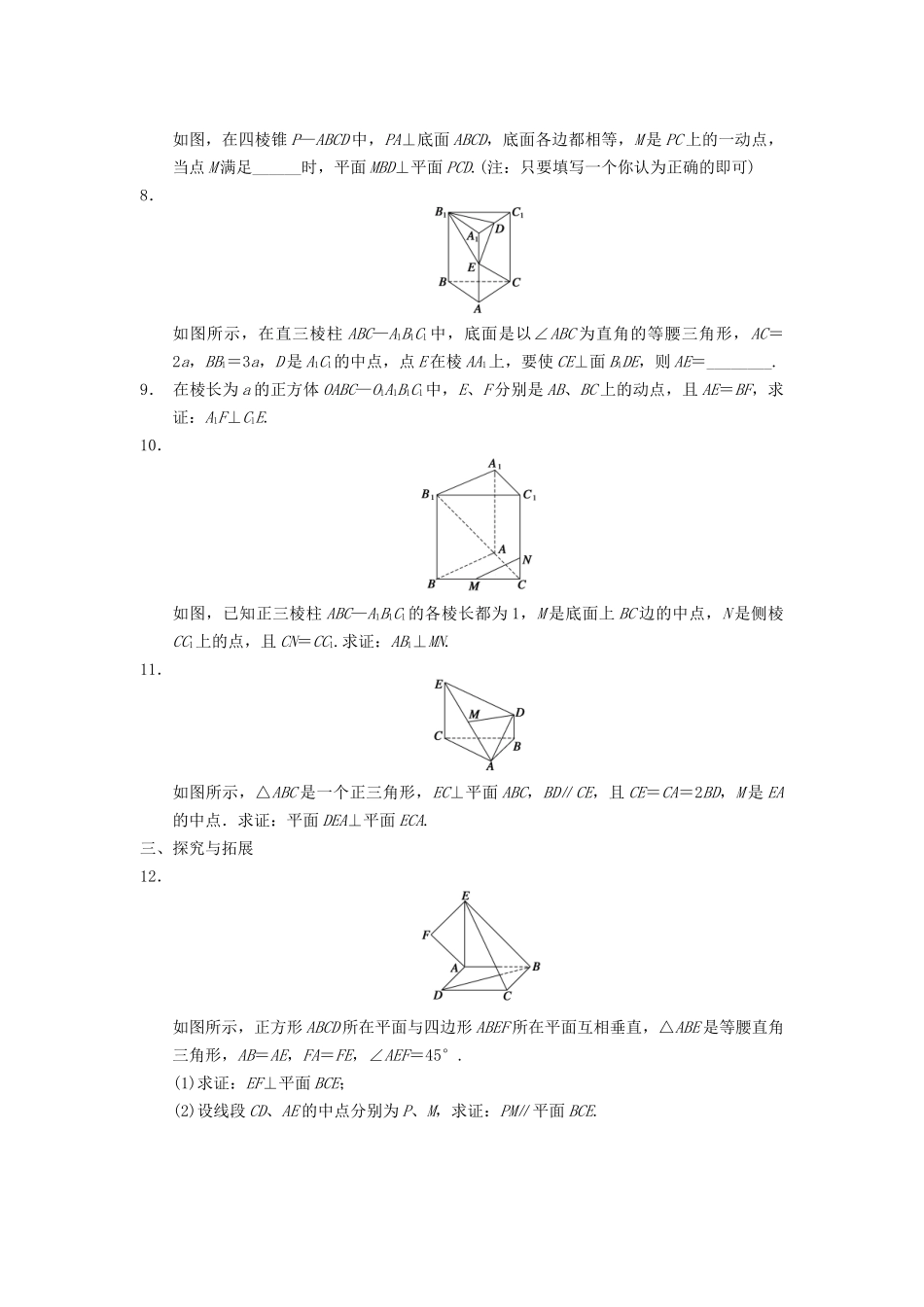
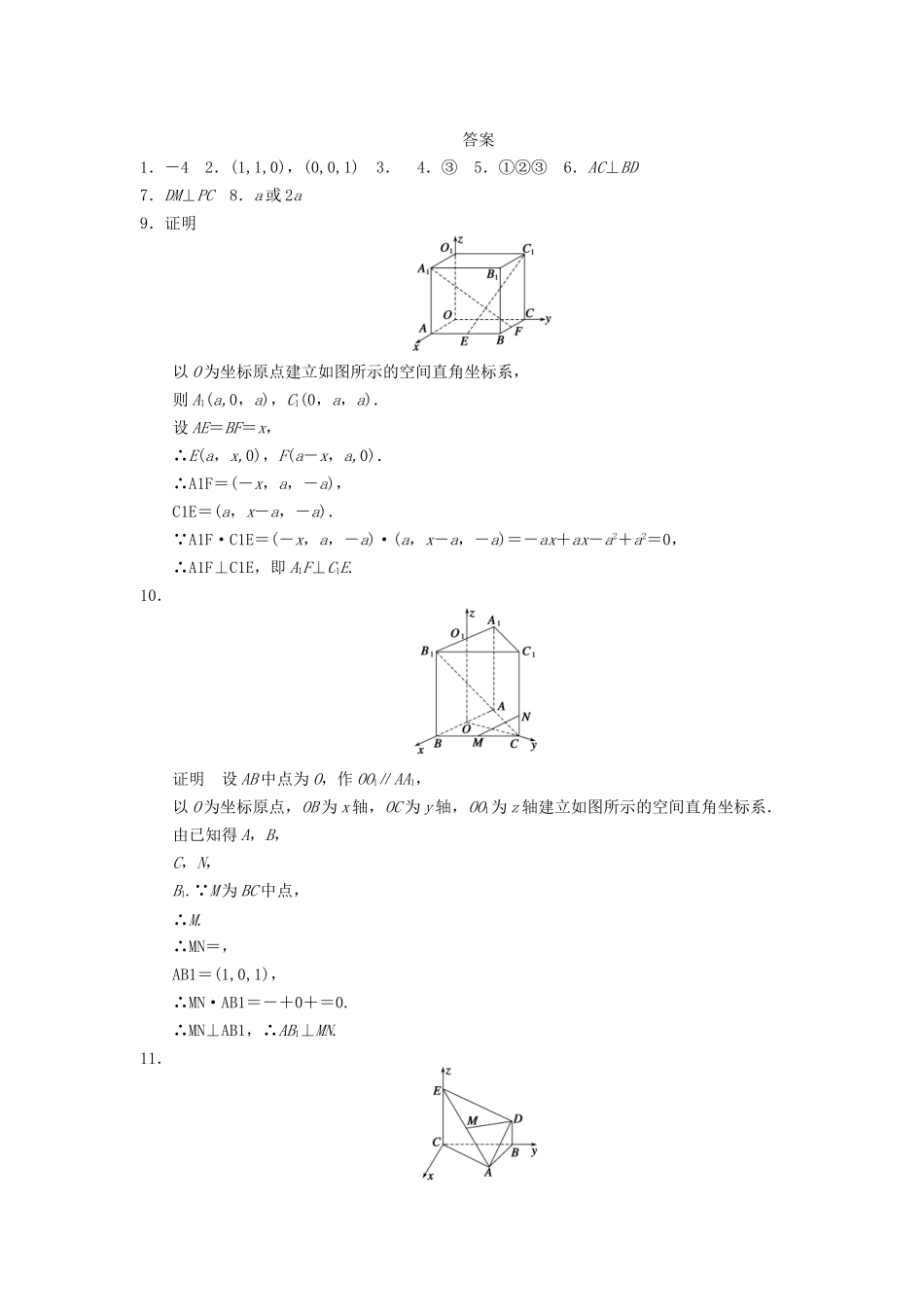
3.2.2空间线面关系的判定(二)——垂直关系的判定一、基础过关1.已知平面α和平面β的法向量分别为a=(1,1,2),b=(x,-2,3),且α⊥β,则x=___.2.已知a=(1,1,0),b=(1,1,1),若b=b1+b2,且b1∥a,b2⊥a,则b1,b2分别为________________.3.已知AB=(1,5,-2),BC=(3,1,z),若AB⊥BC,BP=(x-1,y,-3),且BP⊥平面ABC,则BP=______________.4.下列命题中,正确的命题是________(填序号).①若a是平面α的斜线,直线b垂直于a在α内的射影,则a⊥b;②若a是平面α的斜线,平面β内的直线b垂直于a在α内的射影,则a⊥b;③若a是平面α的斜线,b是平面α内的一条直线,且b垂直于a在α内的射影,则a⊥b;④若a是平面α的射线,直线b平行于平面α,且b垂直于a在另一平面β内的射影,则a⊥b.5.已知点P是平行四边形ABCD所在的平面外一点,如果AB=(2,-1,-4),AD=(4,2,0),AP=(-1,2,-1).对于结论:①AP⊥AB;②AP⊥AD;③AP是平面ABCD的法向量;④AP∥BD.其中正确的是________(填序号).6.如图所示,在直四棱柱A1B1C1D1—ABCD中,当底面四边形ABCD满足条件________时,有A1C⊥B1D1.(注:填上你认为正确的一个条件即可,不必考虑所有可能情形)二、能力提升7.如图,在四棱锥P—ABCD中,PA⊥底面ABCD,底面各边都相等,M是PC上的一动点,当点M满足______时,平面MBD⊥平面PCD.(注:只要填写一个你认为正确的即可)8.如图所示,在直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥面B1DE,则AE=________.9.在棱长为a的正方体OABC—O1A1B1C1中,E、F分别是AB、BC上的动点,且AE=BF,求证:A1F⊥C1E.10.如图,已知正三棱柱ABC—A1B1C1的各棱长都为1,M是底面上BC边的中点,N是侧棱CC1上的点,且CN=CC1.求证:AB1⊥MN.11.如图所示,△ABC是一个正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:平面DEA⊥平面ECA.三、探究与拓展12.如图所示,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.(1)求证:EF⊥平面BCE;(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE.答案1.-42.(1,1,0),(0,0,1)3.4.③5.①②③6.AC⊥BD7.DM⊥PC8.a或2a9.证明以O为坐标原点建立如图所示的空间直角坐标系,则A1(a,0,a),C1(0,a,a).设AE=BF=x,∴E(a,x,0),F(a-x,a,0).∴A1F=(-x,a,-a),C1E=(a,x-a,-a).∵A1F·C1E=(-x,a,-a)·(a,x-a,-a)=-ax+ax-a2+a2=0,∴A1F⊥C1E,即A1F⊥C1E.10.证明设AB中点为O,作OO1∥AA1,以O为坐标原点,OB为x轴,OC为y轴,OO1为z轴建立如图所示的空间直角坐标系.由已知得A,B,C,N,B1.∵M为BC中点,∴M.∴MN=,AB1=(1,0,1),∴MN·AB1=-+0+=0.∴MN⊥AB1,∴AB1⊥MN.11.证明建立如图所示的空间直角坐标系C—xyz,不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(,1,0),B(0,2,0),E(0,0,2),D(0,2,1).所以EA=(,1,-2),CE=(0,0,2),ED=(0,2,-1).分别设面ECA与面DEA的法向量是n1=(x1,y1,z1),n2=(x2,y2,z2),则即解得即解得不妨取n1=(1,-,0),n2=(,1,2),因为n1·n2=0,所以两个法向量相互垂直.所以平面DEA⊥平面ECA.12.证明(1)∵△ABE是等腰直角三角形,AB=AE,∴AE⊥AB,又∵平面ABEF⊥平面ABCD且平面ABEF∩平面ABCD=AB,∴AE⊥平面ABCD,∴AE⊥AD.即AD、AB、AE两两垂直.故建立如图所示的空间直角坐标系,设AB=1,则AE=1,B(0,1,0),D(1,0,0),E(0,0,1),C(1,1,0).∵FA=FE,∠AEF=45°,∴∠AFE=90°,从而F,EF=,BE=(0,-1,1),BC=(1,0,0).∴EF·BE=0,EF·BC=0,∴EF⊥BE,EF⊥BC,又∵BE∩BC=B,∴EF⊥平面BCE.(2)M,P,从而PM=.于是PM·EF=·=0+-=0.∴PM⊥EF.又EF⊥平面BCE,直线PM不在平面BCE内,故PM∥平面BCE.