北京市房山区高三数学第二次模拟考试 理(房山二模，无答案) 试题VIP免费

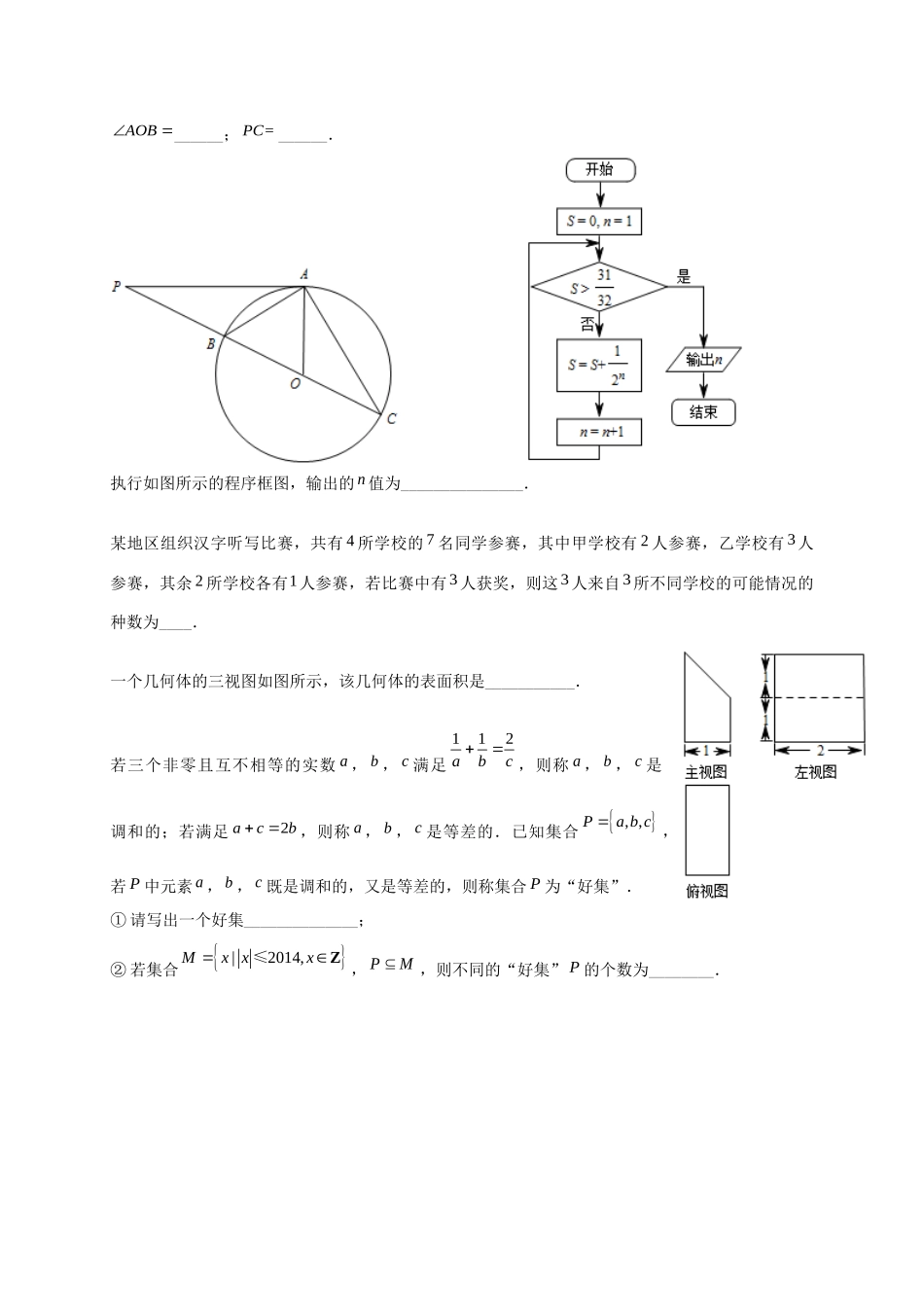
房山2014年高考第二次模拟测试试卷数学（理）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．若aR，i为虚数单位，且ii=1+2ia，则a（）．A．1B．0C．1D．2已知集合|2Axx，集合|ln,1Byyxx，则AB（）．A．2,0B．2,1C．2,D．0,+“1a”是“直线210axy与直线120xay平行”的（）．A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件如图是甲，乙两名同学5次综合测评成绩的茎叶图，下列四个结论中，正确的是（）．A．甲成绩的极差大于乙成绩的极差B．甲成绩的中位数小于乙成绩的中位数C．甲成绩的平均值等于乙成绩的平均值D．甲成绩的标准差小于乙成绩的标准差将函数sin2yx的图像向右平移π8个单位后，所得图象的一条对称轴方程是（）．A．π8xB．π8xC．π4xD．π4x如图，设区域,|0π,01Dxyxy≤≤≤≤，向区域D内随机投入一点，且投入到区域内任一点都是等可能的，则点落入到阴影区,|0π,0sinMxyxyx≤≤≤≤的概率为（）．A．1B．π2C．2πD．1π对任意两实数,ab，定义运算“”：,,,.aababbab≥关于函数1eexxfx给出下列四个结论：①函数fx为偶函数；②函数fx的最小值是e③函数fx在0+，上单调递增④函数fx的图象与直线=e1yx没有公共点其中正确结论的序号是（）．A．①③B．②③C．①④D．②④直线2x与双曲线C：2248xy的渐近线交于,AB两点，设P为双曲线上的任意一点，若OPaOAbOB�（,abR，O为坐标原点），则ab的取值范围是（）．A．,11,B．11,,22C．,22,D．22,,22第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．在极坐标系中，圆=2cos的圆心到直线cos=2的距离为____________．如图，已知PA是圆O的切线，切点为A，PO交圆O于B、C两点，3PA，30PAB，则AOB______；=PC______．执行如图所示的程序框图，输出的n值为_______________．某地区组织汉字听写比赛，共有4所学校的7名同学参赛，其中甲学校有2人参赛，乙学校有3人参赛，其余2所学校各有1人参赛，若比赛中有3人获奖，则这3人来自3所不同学校的可能情况的种数为____．一个几何体的三视图如图所示，该几何体的表面积是___________．若三个非零且互不相等的实数a，b，c满足112abc，则称a，b，c是调和的；若满足2acb，则称a，b，c是等差的．已知集合,,Pabc，若P中元素a，b，c既是调和的，又是等差的，则称集合P为“好集”．①请写出一个好集______________；②若集合|2014,MxxxZ≤，PM，则不同的“好集”P的个数为________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．（本小题共13分）在锐角ABC△中，1cos29C．（I）求sinC的值；（II）当3a，3sin6sinCA时，求b的值．（本小题共14分）如图，在三菱柱111ABCABC中，11AABB为矩形，平面11AABB平面ABC．90ABC，1112ABBCAA，点F为AC的中点，点E为1AA上一点．（I）求证：平面BEF平面11AACC；（II）当AE的长为何值时，二面角111ACEB为60？FEA1B1C1CBA（本小题共13分）甲、乙、丙三人参加一项技能测试，已知甲通过测试的概率为35，乙通过测试的概率为12，乙、丙两人同时通过测试的概率为13，且三人能否通过测试相互独立．（I）求三人中至少一人通过测试的概率；（II）设X为甲、乙、丙三人中通过测试的人数，求X的分布列和数学期望．（本小题共14分）已知函数22()lnafxxaxx．（I）当1a时，求曲线()yfx在点(1,(1))f处的切线方程；（II）讨论函数()fx的单调性；（III）若0a时，函数()fx有两个零点，求a的取值范围．（本小题共13分）已知点(,)Axy和点(4,)By，以AB为直径的圆经过坐标原点O．（I）求点A的轨迹C的方程；（II）过...