高中数学第一轮总复习 第80讲极坐标系及简单的极坐标方程课件(理科)新人教A版 课件VIP免费

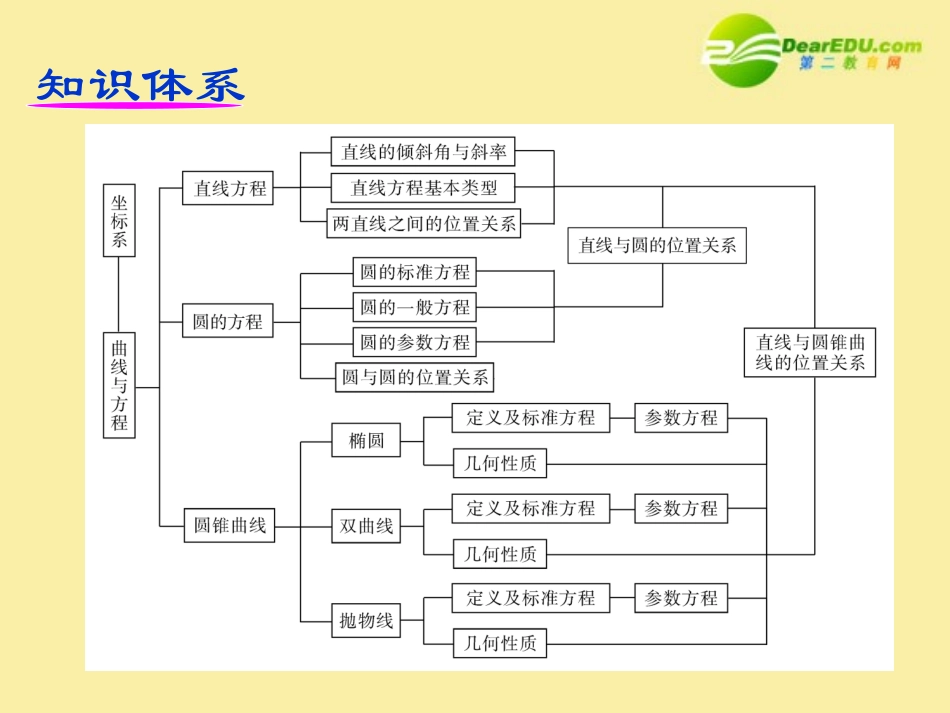
新课标高中一轮新课标高中一轮总复习总复习新课标高中一轮新课标高中一轮总复习总复习理数理数•第十二单元第十二单元•坐标系与方程坐标系与方程知识体系考纲解读1.坐标系.(1)理解坐标系的作用.(2)了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.(3)能在极坐标系中用极坐标表示点的位置，理解在极坐标系和平面直角坐标系中表示点的位置的区别，能进行极坐标与直角坐标的互化.(4)能在极坐标系中给出简单图形（如过极点的直线、过极点或圆心在极点的圆）的方程，通过比较这些图形在极坐标系和平面直角坐标系中的方程，理解用方程表示平面图形时选择适当的坐标系的意义.(5)了解柱坐标系、球坐标系中表示空间中点的位置的方法，并与空间直角坐标系中表示点的位置的方法相比较，了解它们的区别.2.参数方程.(1)了解参数方程，了解参数的意义.(2)能选择适当的参数写出直线、圆和圆锥曲线的参数方程.(3)了解平摆线、渐开线的生成过程，并能推导出它们的参数方程.(4)了解其他摆线生成过程，了解摆线在实际中的应用，了解摆线在表示行星运动轨道中的作用.极坐标系及简单的极坐标方程第第8080讲讲极坐标系及简单的极极坐标系及简单的极坐标方程坐标方程能在极坐标系中用极坐标表示点的位置，能进行极坐标与直角坐标的互化，掌握直线与圆的极坐标方程.1.已知点M(ρ,θ)，则M点关于极点对称的点N的极坐标是()AA.(ρ,π+θ)B.(ρ,-θ)C.(ρ,π-θ)D.(ρ,2π-θ)2.已知点M的直角坐标为(2,-2)，则其极坐标是()BA.(2,)B.(2,-)C.(2,)D.(2,)2342425423.在极坐标系中，过点M(2,)，且平行于极轴的直线的极坐标方程是.ρsinθ=22如图,设P(ρ,θ)为直线上任意一点，在Rt△OMP中，ρcos(-θ)=2,即ρsinθ=2.24.极坐标方程为ρ=2cosθ的圆的半径是.15.极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是.22ρ=cosθ是圆心为(,0)，半径为的圆;ρ=sinθ是圆心为（,）,半径为的圆，故两圆的圆心距为.121212212221.坐标系的类型(1)直线上的点的坐标;(2)平面直角坐标系;(3)①系;(4)柱坐标系;(5)球坐标系.2.坐标之间互化(1)极坐标M(ρ,θ)化为平面直角坐标M(x,y):②.③.极坐标x=ρcosθy=ρsinθ(2)空间点P的直角坐标（x,y,z）与柱坐标(ρ,θ,z)之间的变换公式为：x=ρcosθy=ρsinθz=z.柱坐标系又称半极坐标系，它是由平面极坐标系及空间直角坐标系的一部分建立起来的.(3)空间点P的直角坐标（x,y,z）与球坐标（r,φ,θ）之间的变换关系为x=rsinφcosθy=rsinφsinθz=rcosφ.3.直线与圆的极坐标方程曲线位置极坐标方程直角坐标方程直线过极点，并且与极轴所成的角为αθ=α④.不过极点,和极轴所成的角为α，到极点的距离为p⑤..xsinα-ycosα=py=xtanαρsin(α-θ)=p直线平行于极轴，到极轴的距离为b⑥.y=b垂直于极轴，和极点的距离为aρcosθ=a⑦.过点(ρ1,θ1)，和极轴所成的角为α⑧..y-ρ1sinθ1=tanα(x-ρ1cosθ1)ρsinθ=bx=a1sin()1sin()圆圆心在极点,半径为r⑨.x2+y2=r2圆心为(±r,0),半径为rρ=±2rcosθ⑩.圆心为（r,±),半径为r..x2+y2±2ry=0ρ=rx2±2rx+y2=0211ρ=±2rsinθ题型一点的极坐标表示题型一点的极坐标表示例1典例精讲典例精讲典例精讲典例精讲点P（-,）与曲线C:ρ=sin的关系是.12432因为点P(-,)与点P′(,)是同一点,且sin=sin=,所以点P′在曲线C:ρ=sin上，故点P(－,)在曲线C:ρ=sin上.124312332612212432点A(ρ，θ)（ρ>0），则点A的极坐标的一般形式为A(ρ,θ+2kπ)或(-ρ，θ+(2k+1)π)(k∈Z).点评点评变式变式变式点A（5，）在条件：(1)ρ>0,θ(-2∈π,0)下的极坐标是;(2)ρ<0,θ(2∈π,4π)下的极坐标是.3(1)当ρ＞0时，点A（5，)的极坐标的一般形式为(5,+2kπ)(k∈Z).由-2π＜θ＜0,得-2π＜+2kπ＜0(k∈Z),解得k=-1,所以θ=-2π=-,所以满足条件的点A的极坐标为(5,-).33335353(5,-)53(5,-)103（2）当ρ＜0时，点A（5，)的极坐标的一般形式是(-5，+(2k+1)π)(k∈Z).由2π＜θ＜4π,得2π＜+(2k+1)π＜4π,解得k=1,所以θ=+3π=,故满足条件的点A的极坐标为(-5,).3103333103题型二...