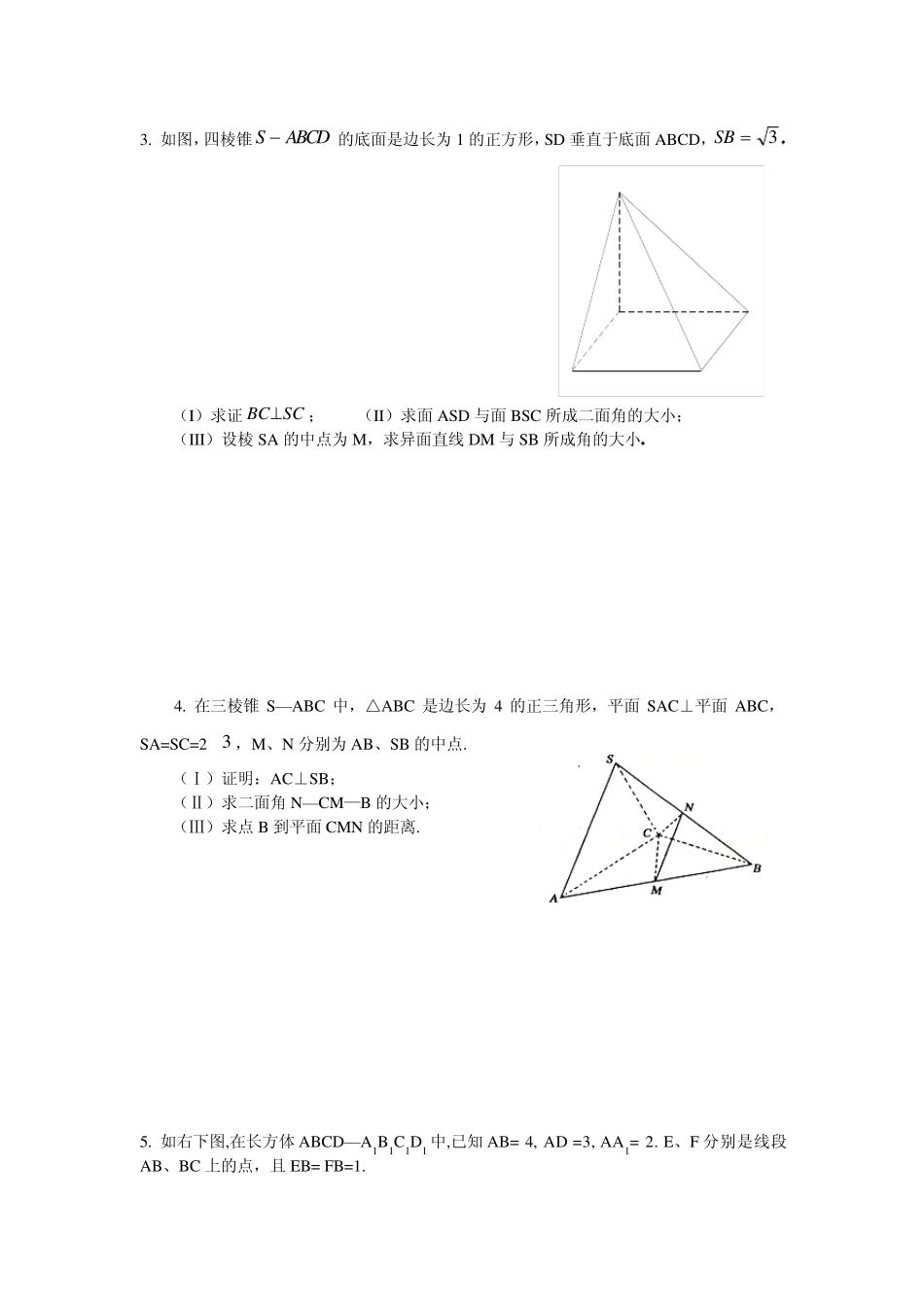
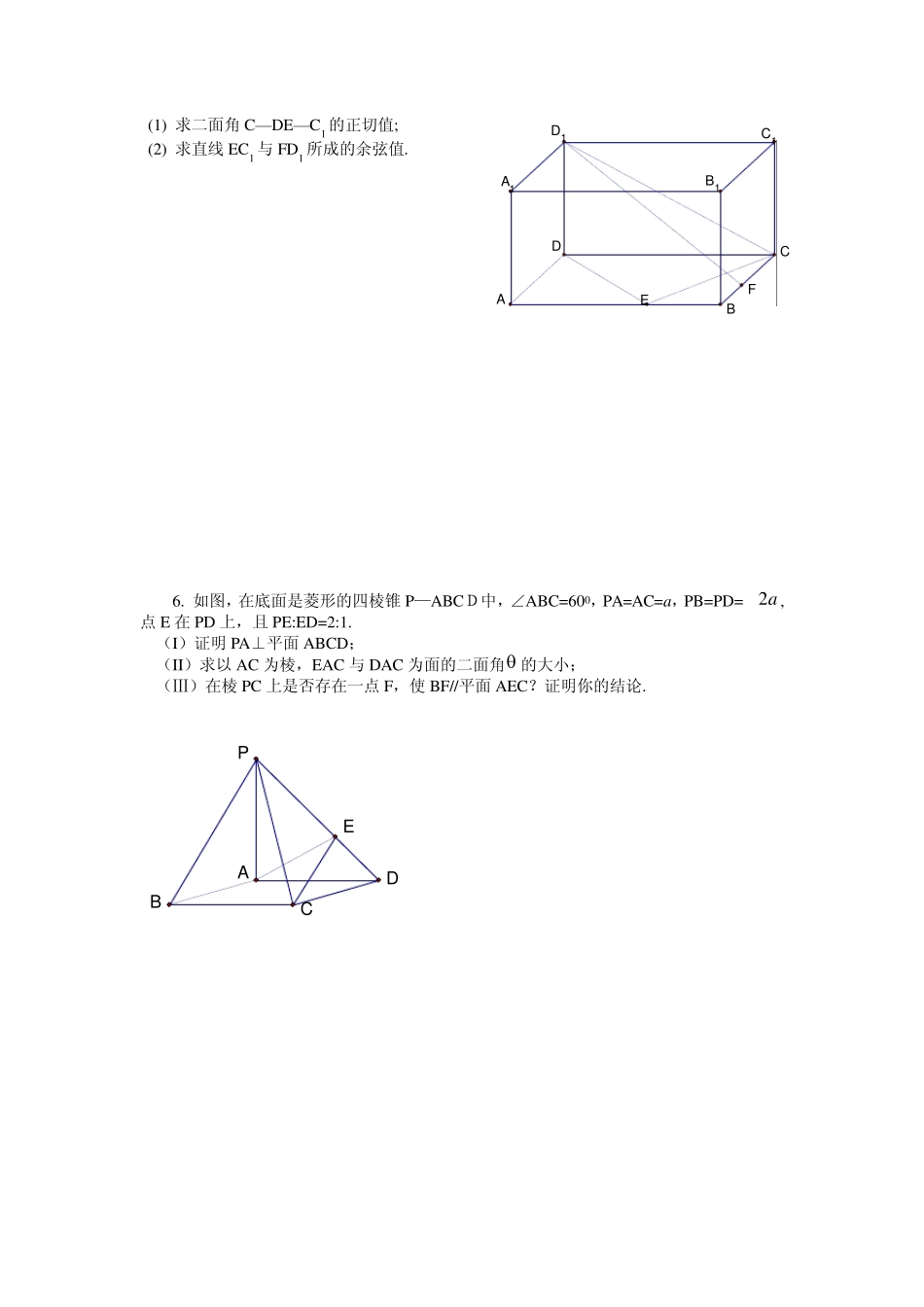
2006 年高考专项训练------立体几何 1. 如图,四棱锥P-ABCD的底面是正方形, ,,//,PAABCD AEPD EFCD AMEF底面 (1) 证明MF是异面直线AB与PC的公垂线; (2) 若3PAAB,求直线AC 与平面EAM 所成角的正弦值 2. 已知三棱柱ABC-A1B1C1 中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=26a, (Ⅰ)求异面直线AC 与BC1 所成角的余弦值; (Ⅱ)求证:A1B⊥面AB1C. BCDAPMFE3. 如图,四棱锥SABCD的底面是边长为1 的正方形,SD 垂直于底面ABCD,SB 3 DABSC (I)求证BC SC; (II)求面ASD 与面BSC 所成二面角的大小; (III)设棱SA 的中点为M,求异面直线DM 与SB 所成角的大小 4. 在三棱锥S—ABC 中,△ABC 是边长为4 的正三角形,平面SAC⊥平面ABC,SA=SC=2 3 ,M、N 分别为AB、SB 的中点. (Ⅰ)证明:AC⊥SB; (Ⅱ)求二面角N—CM—B 的大小; (Ⅲ)求点B 到平面CMN 的距离. 5. 如右下图,在长方体 ABCD—A1B1C1D1 中,已知 AB= 4, AD =3, AA1= 2. E、F 分别是线段AB、BC 上的点,且 EB= FB=1. (1) 求二面角C—DE—C1 的正切值; (2) 求直线EC1 与FD1 所成的余弦值. 6. 如图,在底面是菱形的四棱锥P —ABCD中,∠ABC=600,P A=AC=a,P B=P D=a2 ,点 E 在P D 上,且 P E:ED=2:1. (I)证明 PA⊥平面ABCD; (II)求以 AC 为棱,EAC 与DAC 为面的二面角 的大小; (Ⅲ)在棱P C 上是否存在一点 F,使 BF//平面AEC?证明你的结论. BCDAPE D1C1B1CDBAA1EF 7. 在棱长为4 的正方体ABCD-A1B1C1D1 中,O 是正方形A1B1C1D1 的中心,点P在棱CC1上,且CC1=4CP. (Ⅰ)求直线AP与平面BCC1B1 所成的角的大小(结果用反三角函数值表示); (Ⅱ)设O 点在平面D1AP上的射影是H,求证:D1H⊥AP; (Ⅲ)求点P到平面ABD1 的距离. 8. 如图,已知四棱锥 P—ABCD,PB⊥AD 侧面PAD 为边长等于2 的正三角形,底面ABCD 为菱形,侧面PAD 与底面ABCD 所成的二面角为120°. (I)求点P到平面ABCD 的距离, (II)求面APB 与面CPB 所成二面角的大小. · B1 P A C D A1 C1 D1 B O H · 9. 如图,直三棱柱ABC-A1B1C1 中,∠ACB=90o,AC=1,CB=2 ,侧棱AA1=1,侧面AA1B1B 的两条对角线交点为D,B1C1 的中点为M. (Ⅰ)求证:CD⊥平面BDM; (Ⅱ)求面B1BD 与面CBD 所成二面角的大小. 10. 三棱锥 P-ABC...