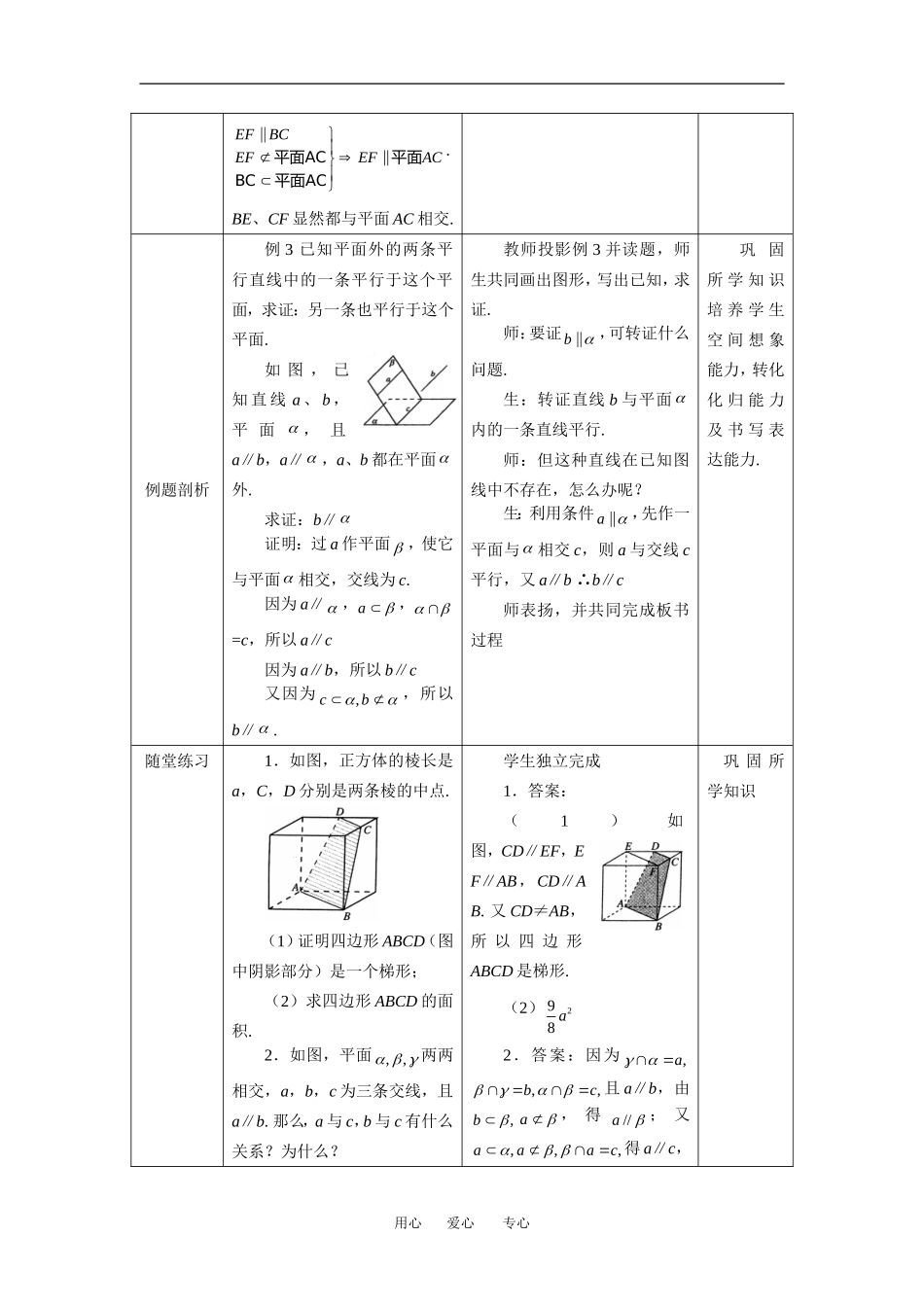
第二课时 直线与平面平行的性质（一）教学目标1．知识与技能掌握直线与平面平行的性质定理及其应用
2．过程与方法学生通过观察与类比，借助实物模型性质及其应用
3．情感、态度与价值观（1）进一步提高学生空间想象能力、思维能力
（2）进一步体会类比的作用
（3）进一步渗透等价转化的思想
（二）教学重点、难点重点：直线和平面平行的性质
难点：性质定理的证明与灵活运用
（三）教学方法讲练结合教学过程教学内容师生互动设计意图新课导入1．直线与平面平行的判定定理2．直线与平面的位置关系3．思考：如果直线和平面平行、那么这条直线与这个平面内的直线是有什么位置关系
投影幻灯片，师生共同复习，并讨论思考题
复习巩固探索新知直线与平面平行的性质1．思考题：一条直线与一个平面平行，那么在什么条件下，平面 内的直线与这条直线平行
2．例 1 如图 a∥ a ，= b
求证：a∥b
证明：因为=b，所以b
因为 a∥ ，所以 a 与 b 无公共点
师：投影问题，学生回答
生：当平面内的直线与这条直线共面时两条直线平行
生：由条件知两条直线没有公共点，如果它们共面，那么它们一定平行
师投影例 1 并读题，学生分析，教师板书，得出定理
师：直线与平面平行的性质定理揭示了直线与平面平行中蕴含直线与直线平行
通过直线与平面平行可得到直线与直通 过讨 论 板 书加 深 对 知识的理解
培 养 学 生书 写 的 能力
用心 爱心 专心又因为,b，所以a∥b
3．定理 一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行
简证为：线面平行则线线平行
符号表示：aaabab 线平行，这给出了一种作平行线的重要方法
典例剖析例 2 如图所示的一块林料中，棱 BC 平行平面 A′C′
（1）要经过面 A′C′内一的点
