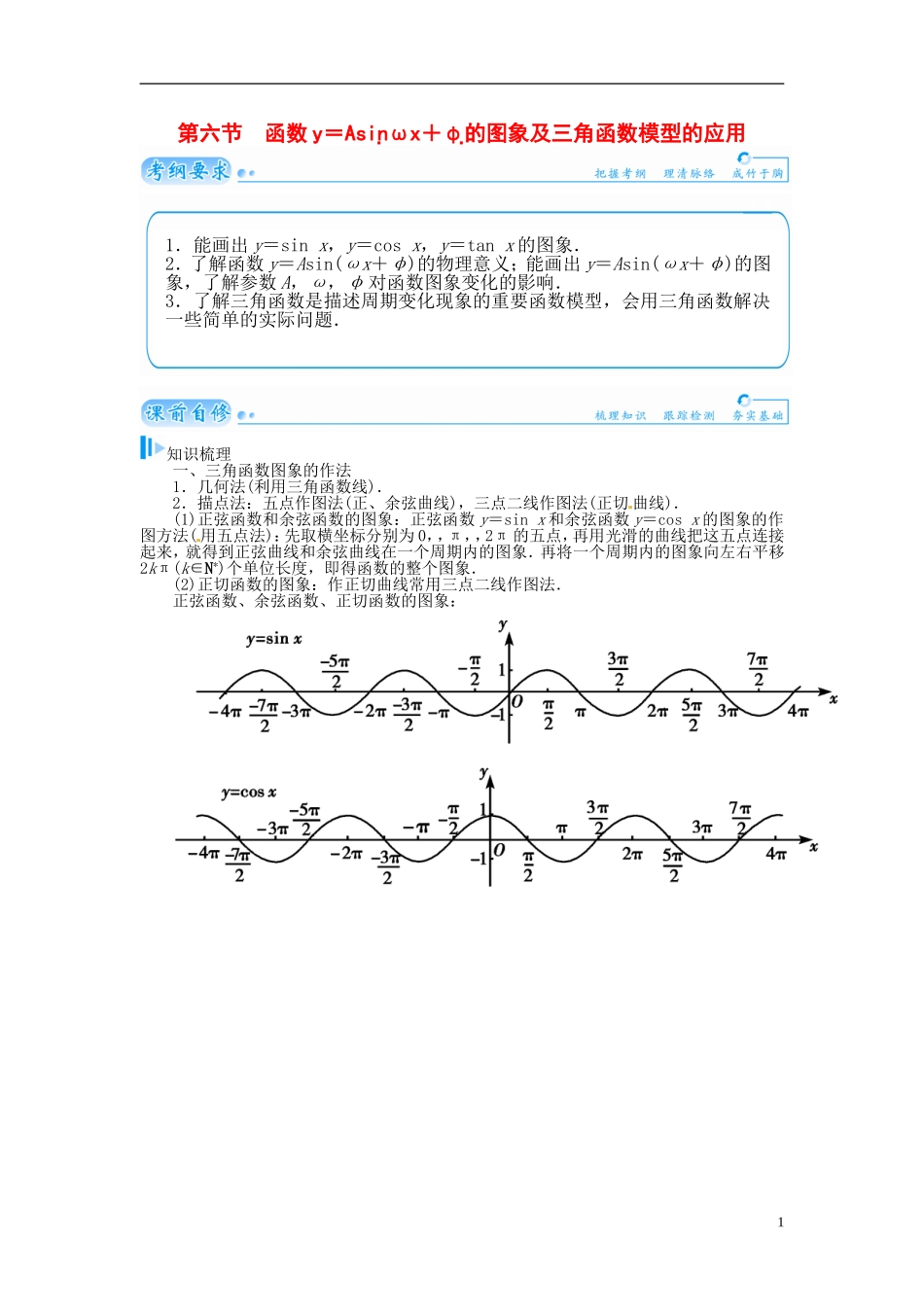
第六节 函数 y=Asinωx+φ的图象及三角函数模型的应用知识梳理一、三角函数图象的作法1.几何法(利用三角函数线).2.描点法:五点作图法(正、余弦曲线),三点二线作图法(正切 曲线).(1)正弦函数和余弦函数的图象:正弦函数 y=sin x 和余弦函数 y=cos x 的图象的作图方法( 用五点法):先取横坐标分别为 0,,π,,2π 的五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象.再将一个周期内的图象向左右平移2kπ(k∈N*)个单位长度,即得函数的整个图象.(2)正切函数的图象:作正切曲线常用三点二线作图法.正弦函数、余弦函数、正切函数的图象:11.能画出 y=sin x,y=cos x,y=tan x 的图象.2.了解函数 y=Asin(ωx+φ)的物理意义;能画出 y=Asin(ωx+φ)的图象,了解参数 A,ω,φ 对函数图象变化的影响.3.了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单的实际问题.图象与 x 轴的交点:正弦函数为________,k∈Z,余弦函数为________,k∈Z,正切函 数为________ ,k∈Z.答案:2.(2)(kπ,0) (kπ,0)二、三角函数图象的对称轴与对称中心正弦曲线 y=sin x 的对称轴为 x=________(k∈Z),对称中心为________(k∈Z);余弦曲线 y=cos x 的对称轴为 x=________(k∈Z);对称中心为________,(k∈Z);正切曲线 y=tan x 的对称中心为________(k∈Z).其 中,正弦函数与余弦函数在对称轴与曲线交点处有最大(小)值.答案:kπ+ (kπ,0) kπ 三、函数 y=Asin(ωx+φ)图象的画法1.五点法作 y=Asin(ωx+φ)(A>0,ω>0)的简图.设 X=ωx+φ,由 X 取 0,,π,,2π 来求相应的 x 值及对应的 y 值,再描点作图.2.正弦型函数 y=Asin(ωx+φ)+B(其中 A>0,ω>0)的一些结论:最大值是 A+B,最小值是 B-A,周期是 T=,频率是 f=,相位是 ωx+φ,初相是 φ(即当 x=0 时的相位);其图象的对称轴是直线 ωx+φ=kπ+(k∈Z),凡是该图象与直线 y=B 的交点都是该图象的对称中心.对于 y=Asin(ωx+φ)和 y =Acos(ωx+φ)来说,对称中心与零点相联系,对称轴与最值点相联系.3.利用图象变换作三角函数的图象.三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数 y=Asin(ωx+φ)+B 的作法.(1)________或叫做沿 y 轴的伸缩变换:由 y=sin x 的图象上...