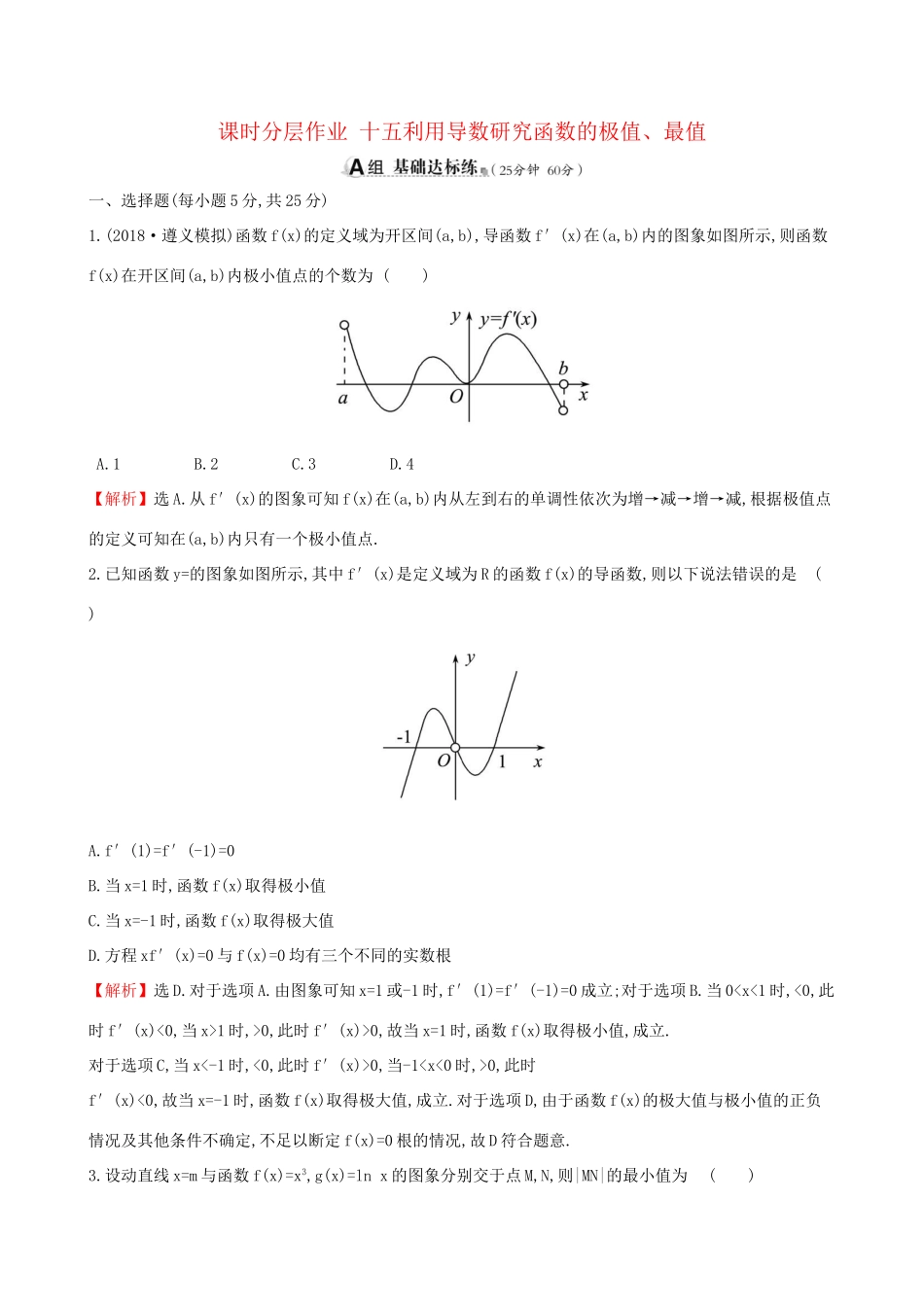
课时分层作业十五利用导数研究函数的极值、最值一、选择题(每小题5分,共25分)1.(2018·遵义模拟)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内极小值点的个数为()A.1B.2C.3D.4【解析】选A.从f′(x)的图象可知f(x)在(a,b)内从左到右的单调性依次为增→减→增→减,根据极值点的定义可知在(a,b)内只有一个极小值点.2.已知函数y=的图象如图所示,其中f′(x)是定义域为R的函数f(x)的导函数,则以下说法错误的是()A.f′(1)=f′(-1)=0B.当x=1时,函数f(x)取得极小值C.当x=-1时,函数f(x)取得极大值D.方程xf′(x)=0与f(x)=0均有三个不同的实数根【解析】选D.对于选项A.由图象可知x=1或-1时,f′(1)=f′(-1)=0成立;对于选项B.当0
1时,>0,此时f′(x)>0,故当x=1时,函数f(x)取得极小值,成立.对于选项C,当x<-1时,<0,此时f′(x)>0,当-10,此时f′(x)<0,故当x=-1时,函数f(x)取得极大值,成立.对于选项D,由于函数f(x)的极大值与极小值的正负情况及其他条件不确定,不足以断定f(x)=0根的情况,故D符合题意.3.设动直线x=m与函数f(x)=x3,g(x)=lnx的图象分别交于点M,N,则|MN|的最小值为()A.(1+ln3)B.ln3C.1+ln3D.ln3-1【解析】选A.设F(x)=f(x)-g(x)=x3-lnx,求导得:F′(x)=3x2-.令F′(x)>0得x>;令F′(x)<0得0g(1)=1,又因为0<α<,所以α∈.4.(2018·长沙模拟)已知函数f(x)=x3-3ax2-9a2x+a3.若a>,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为()A.B.C.D.【解析】选A.f′(x)=3x2-6ax-9a2的图象是一条开口向上的抛物线,关于x=a对称.若1,则因为|f′(a)|=15a2>12a.故当x∈[1,4a]时|f′(x)|≤12a不恒成立.所以使|f′(x)|≤12a(x∈[1,4a])恒成立的a的取值范围是.5.(2018·昆明模拟)已知函数f(x)=-lnx,f(x)在x=x0处取得最大值,以下各式中:①f(x0)x0;④f(x0)<;⑤f(x0)>,正确的序号是()A.③⑤B.②⑤C.①④D.②④【解析】选D.求导函数可得:f′(x)=-,令g(x)=x+1+lnx,则函数有唯一零点x0,所以-x0-1=lnx0,所以f(x0)=(-x0-1)=x0,即②正确;f(x0)-=,因为-x0-1=lnx0,所以f(x0)-=,当x=时,f′=-<0=f′(x0),所以x0在x=左侧,所以x0<,所以1-2x0>0,所以<0,所以f(x0)<,所以④正确.综上知,②④正确.二、填空题(每小题5分,共15分)6.已知函数f(x)=aln2x+bx在x=1处取得最大值ln2-1,则a=________,b=________.【解析】f′(x)=+b=(x>0),当f′(x)=0时,x=-,当x=1时,函数取得最大值ln2-1,即解得a=1,b=-1.答案:1-17.(2018·济南模拟)f(x)=x(x-c)2在x=2处有极大值,则常数c的值为________.【解析】f(x)=x3-2cx2+c2x,f′(x)=3x2-4cx+c2,f′(2)=0⇒c=2或c=6.若c=2,f′(x)=3x2-8x+4,令f′(x)>0⇒x<或x>2,f′(x)<0⇒