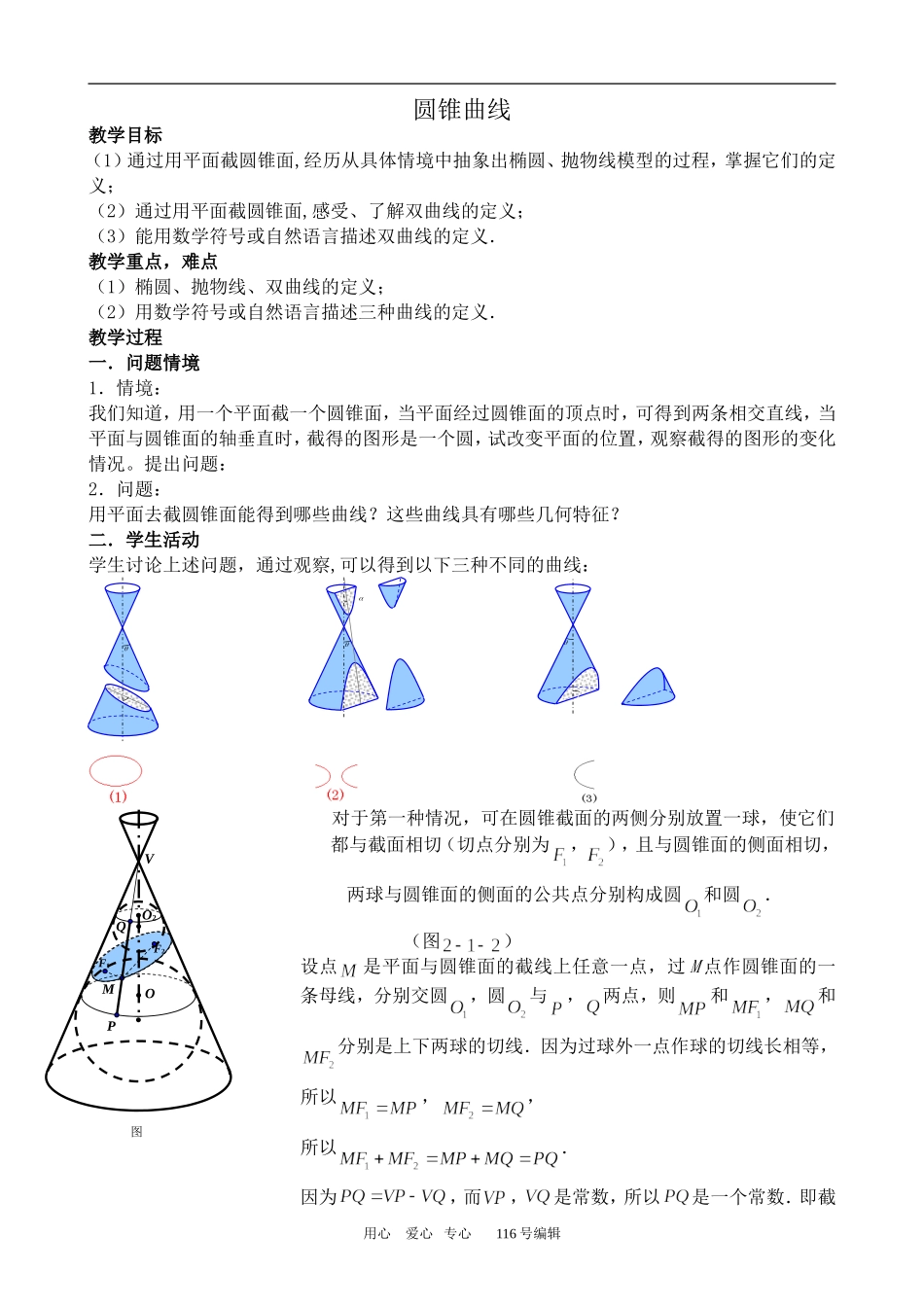
圆锥曲线教学目标(1)通过用平面截圆锥面,经历从具体情境中抽象出椭圆、抛物线模型的过程,掌握它们的定义;(2)通过用平面截圆锥面,感受、了解双曲线的定义;(3)能用数学符号或自然语言描述双曲线的定义.教学重点,难点(1)椭圆、抛物线、双曲线的定义;(2)用数学符号或自然语言描述三种曲线的定义.教学过程一.问题情境1.情境:我们知道,用一个平面截一个圆锥面,当平面经过圆锥面的顶点时,可得到两条相交直线,当平面与圆锥面的轴垂直时,截得的图形是一个圆,试改变平面的位置,观察截得的图形的变化情况。提出问题: 2.问题:用平面去截圆锥面能得到哪些曲线?这些曲线具有哪些几何特征?二.学生活动学生讨论上述问题,通过观察,可以得到以下三种不同的曲线: 对于第一种情况,可在圆锥截面的两侧分别放置一球,使它们 都与截面相切(切点分别为,),且与圆锥面的侧面相切, 两球与圆锥面的侧面的公共点分别构成圆和圆.(图)设点是平面与圆锥面的截线上任意一点,过 M 点作圆锥面的一条母线,分别交圆,圆与,两点,则和,和分别是上下两球的切线.因为过球外一点作球的切线长相等,所以,,所以.因为,而,是常数,所以是一个常数.即截用心 爱心 专心 116 号编辑MQF2PO1O2图VF1线上任意一点到两个定点,的距离的和等于常数.说明:对用 Dandelin 双球理论发现椭圆的特性,可直接给出放进双球后的图形,再由学生发现"到两点距离之和为定值"的特征,可以直接演示说明,不必花费过多时间和精力,只要让学生感知、认同即可.三.建构数学1.椭圆的定义:平面内到两定点,的距离和等于常数(大于)的点的轨迹叫做椭圆,两个定点,叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.说明:(1)定义中的定值要大于,否则不是椭圆.若定值等于,则点的轨迹是线段;若定值小于,则点的轨迹不存在.(2)建议对与 Dandelin 双球理论可作简单介绍,主要利用把细绳两个端点分别固定在,点,用笔尖把绳子拉紧,使笔尖在图板上移动,画出椭圆,来帮助学生理解椭圆的定义.2.双曲线的定义:(类比椭圆的定义)平面内到两定点,的距离的差的绝对值等于常数(大于,小于)的点的轨迹叫做双曲线,两个定点,叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.说明:定义中的定值要小于,否则不是双曲线.若定值等于,则点的轨迹为线段的中垂线;若定值等于,则点的轨迹是两条射线;若定值大于,则点的轨迹不存...