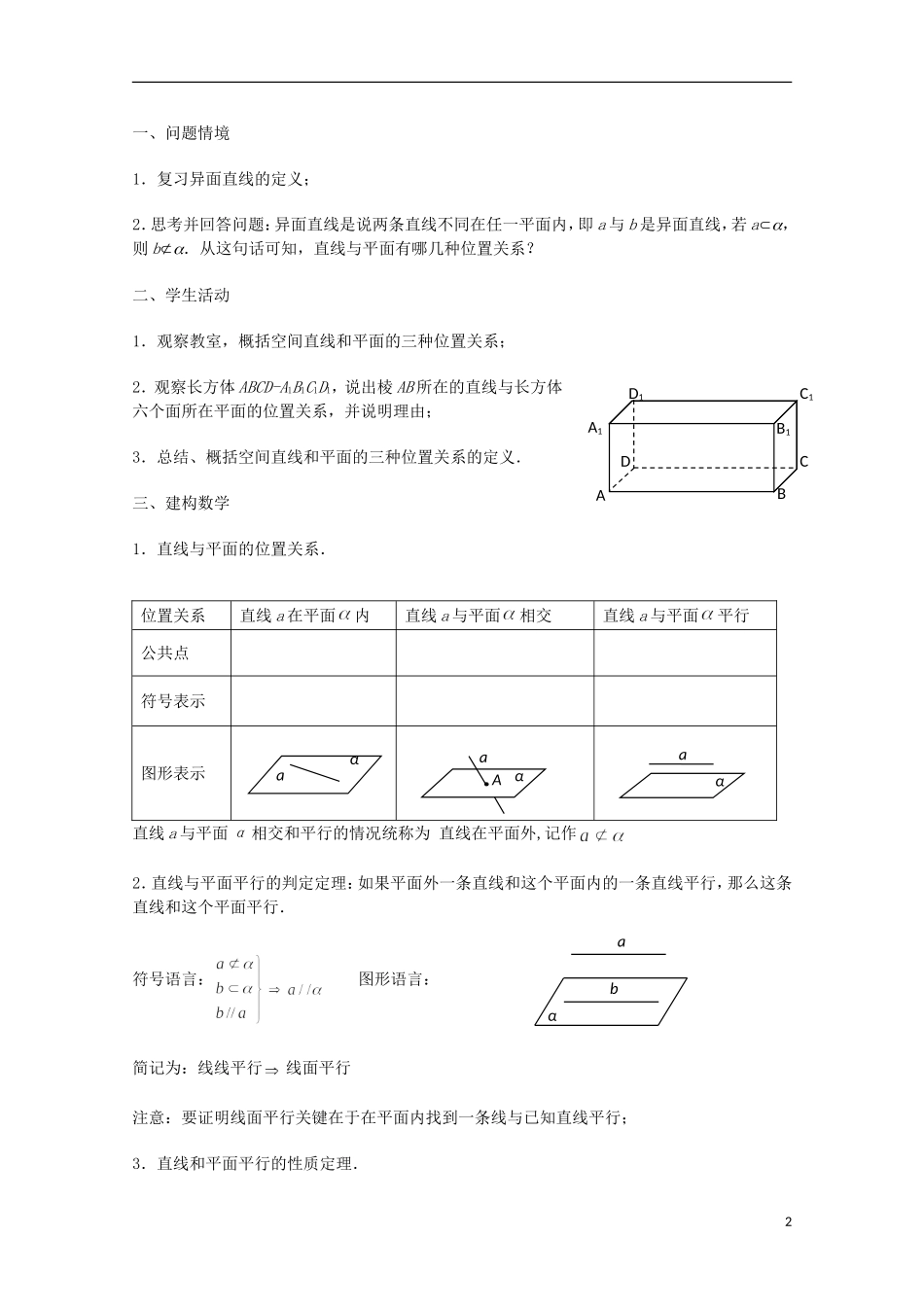
1.2.3 直线与平面的位置关系(1)教学目标:1. 了解空间中直线与平面的位置关系及分类标准;2. 掌握直线与平面平行的判定定理及性质定理,会应用它证明有关的问题;3. 在引导学生观察、分析、抽象、类比得出空间直线与平面位置关系的过程中,努力渗透数学思想及辨证唯物主义观念.教材分析及教材内容的定位:直线与平面的位置关系是高考重点考查内容之一,解决问题的关键是根据线与面之间的互化关系,借助创设辅助线与平面.通过对有关概念和定理的概括、证明和应用,使学生体会“转化”的思想,提高学生的空间想象能力和逻辑推理能力.本节课的主要内容是直线与平面平行的判定定理和性质定理的探究与发现、概括与证明、练习与应用.欲证线面平行,需转化为线线平行,故线面平行判定是线线平行判定的上位知识,需要认真复习初中平几中线线平行的有关内容;而已知线面平行时需要构造辅助平面与已知平面相交,则得出线线平行.线面平行判定是三大平行判定(线线平行、线面平行、面面平行)的核心,也是高考的高频考点之一,学好线面平行对后续学习面面平行及三大垂直的判定与性质等内容,具有良好的示范作用.学习这些内容是培养学生的数学表述与交流能力(用集合符号语言进行数学表达与交流),直感思维与逻辑思维,推理论证能力及空间想象能力等的重要载体.线面平行的判定蕴含的数学思想方法主要有数形结合、化归与转化思想.教学重点:直线和平面的位置关系,直线和平面平行的判定定理以及性质定理.教学难点:直线和平面平行的判定定理以及性质定理的正确运用.教学方法:探究发现式、合作讨论式教学过程:1一、问题情境1.复习异面直线的定义;2.思考并回答问题:异面直线是说两条直线不同在任一平面内,即 a 与 b 是异面直线,若 aÌa,则 bËa.从这句话可知,直线与平面有哪几种位置关系? 二、学生活动1.观察教室,概括空间直线和平面的三种位置关系;2.观察长方体 ABCD-A1B1C1D1,说出棱 AB 所在的直线与长方体六个面所在平面的位置关系,并说明理由;3.总结、概括空间直线和平面的三种位置关系的定义.三、建构数学1.直线与平面的位置关系.直线 a 与平面 α 相交和平行的情况统称为 直线在平面外,记作2.直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.符号语言: 图形语言:简记为:线线平行线面平行注意:要证明线面平行关键在于在平面内找到一...