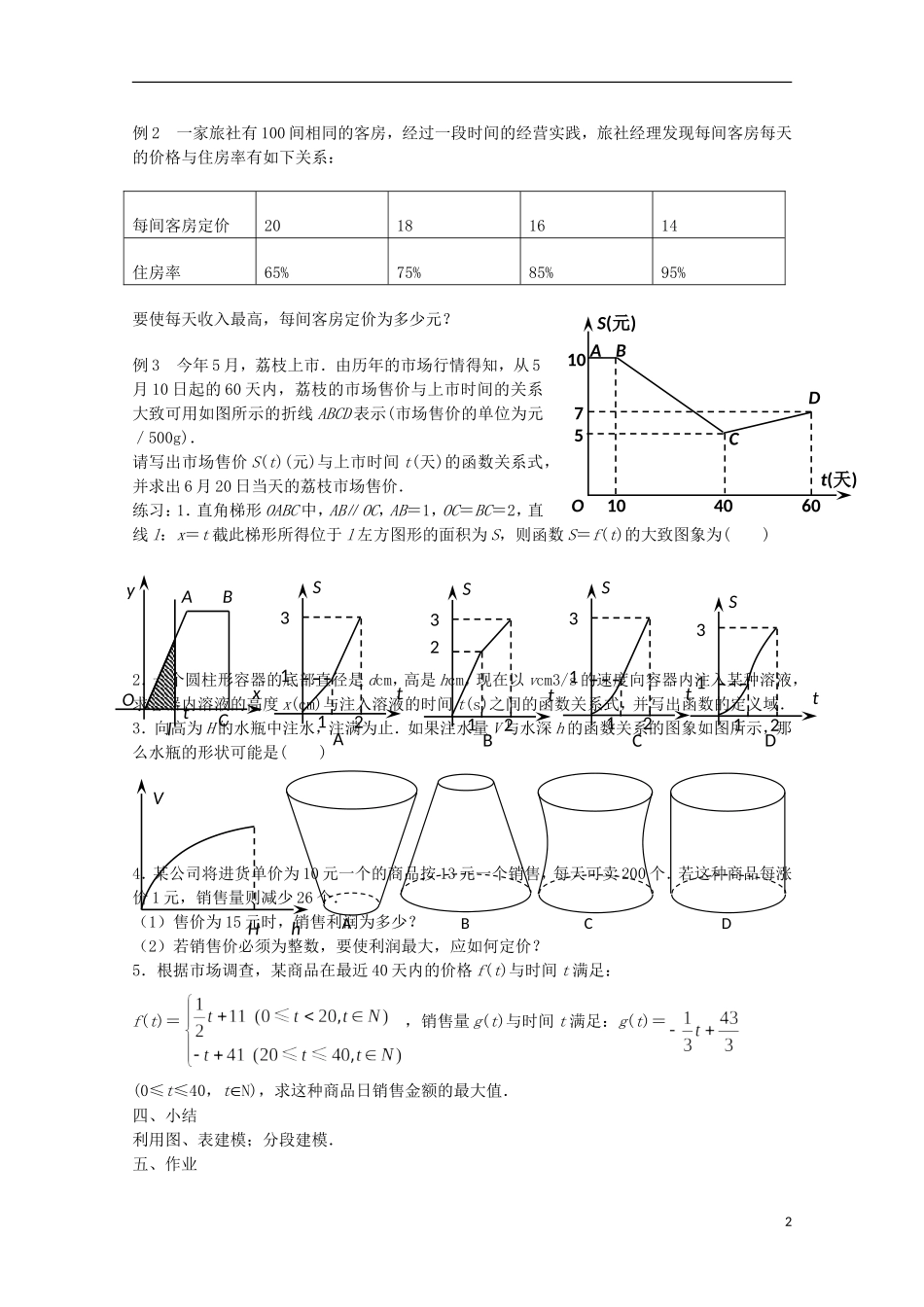
3.4.2 函数模型及其应用(2)教学目标:1.能根据图形、表格等实际问题的情境建立数学模型,并求解;进一步了解函数模型在解决简单的实际问题中的应用,了解函数模型在社会生活中的广泛应用;2.在解决实际问题的过程中,培养学生数学地分析问题、探索问题、解决问题的能力,培养学生的应用意识,提高学习数学的兴趣.教学重点:在解决以图、表等形式作为问题背景的实际问题中,读懂图表并求解.教学难点:对图、表的理解.教学方法:讲授法,尝试法.教学过程:一、情境创设已知矩形的长为 4,宽为 3,如果长增加 x,宽减少 0.5x,所得新矩形的面积为 S.(1)将 S 表示成 x 的函数;(2)求面积 S 的最大值,并求此时 x 的值.二、学生活动思考并完成上述问题.三、例题解析例 1 有一块半径为 R 的半圆形钢板,计划剪裁成等腰梯形ABCD 的形状,它的下底 AB 是⊙O 的直径,上底 CD 的端点在圆周上,写出这个梯形周长 y 和腰长 x 间的函数关系式,并求出它的定义域. 1ABOCDE例 2 一家旅社有 100 间相同的客房,经过一段时间的经营实践,旅社经理发现每间客房每天的价格与住房率有如下关系:每间客房定价20181614住房率65%75%85%95%要使每天收入最高,每间客房定价为多少元?例 3 今年 5 月,荔枝上市.由历年的市场行情得知,从 5月 10 日起的 60 天内,荔枝的市场售价与上市时间的关系大致可用如图所示的折线 ABCD 表示(市场售价的单位为元/500g).请写出市场售价 S(t)(元)与上市时间 t(天)的函数关系式,并求出 6 月 20 日当天的荔枝市场售价.练习:1.直角梯形 OABC 中,AB∥OC,AB=1,OC=BC=2,直线 l:x=t 截此梯形所得位于 l 左方图形的面积为 S,则函数 S=f(t)的大致图象为( )2.一个圆柱形容器的底部直径是 dcm,高是 hcm,现在以 vcm3/s 的速度向容器内注入某种溶液,求容器内溶液的高度 x(cm)与注入溶液的时间 t(s)之间的函数关系式,并写出函数的定义域. 3.向高为 H 的水瓶中注水,注满为止.如果注水量 V 与水深 h 的函数关系的图象如图所示,那么水瓶的形状可能是( )4.某公司将进货单价为 10 元一个的商品按 13 元一个销售,每天可卖 200 个.若这种商品每涨价 1 元,销售量则减少 26 个.(1)售价为 15 元时,销售利润为多少?(2)若销售价必须为整数,要使利润最大,应如何定价? 5.根据市场调查,某商品在最近 40 天内的价格 f...