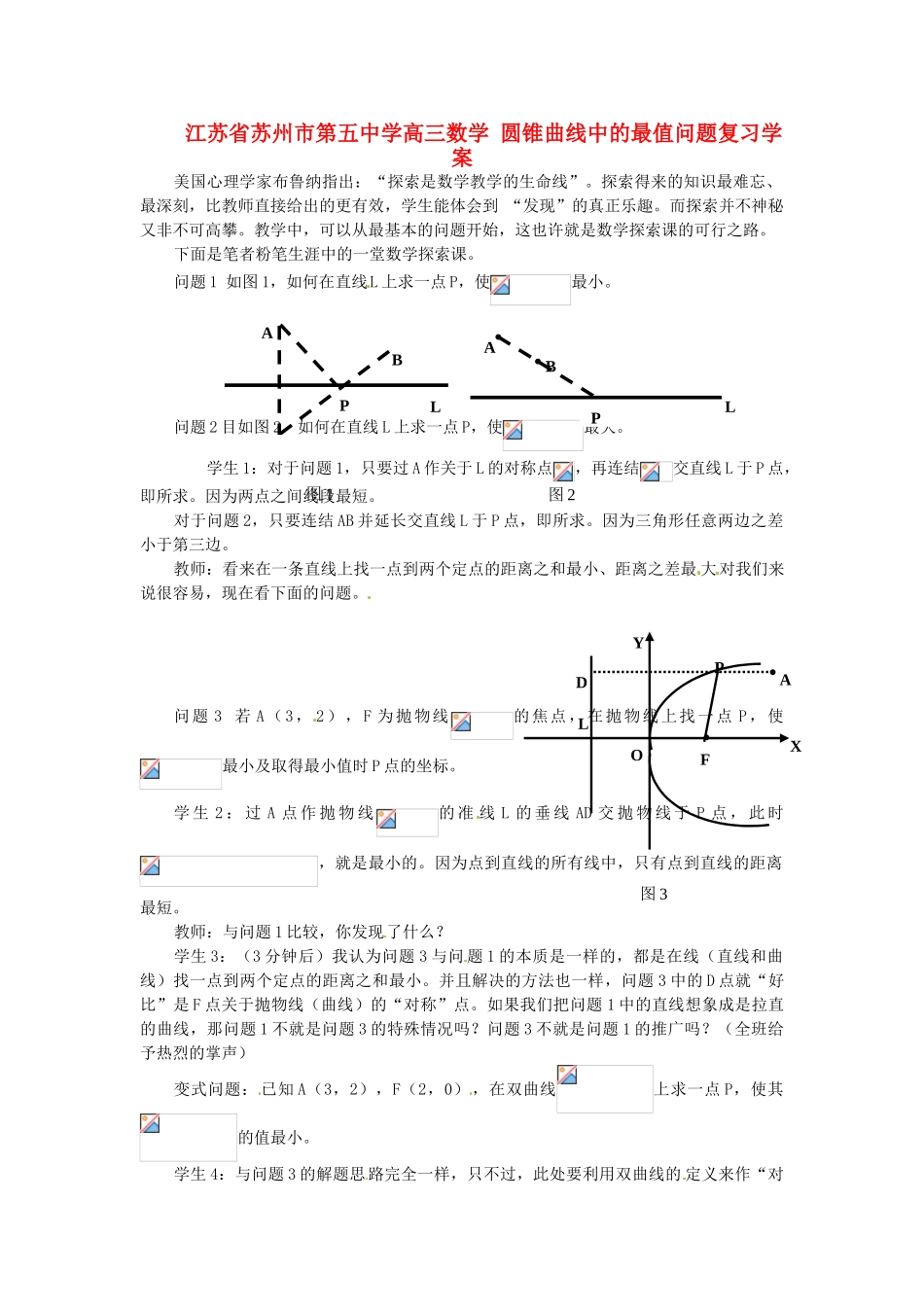
江苏省苏州市第五中学高三数学 圆锥曲线中的最值问题复习学案美国心理学家布鲁纳指出:“探索是数学教学的生命线”。探索得来的知识最难忘、最深刻,比教师直接给出的更有效,学生能体会到 “发现”的真正乐趣。而探索并不神秘又非不可高攀。教学中,可以从最基本的问题开始,这也许就是数学探索课的可行之路。下面是笔者粉笔生涯中的一堂数学探索课。问题 1 如图 1,如何在直线L 上求一点 P,使最小。问题 2 目如图 2,如何在直线 L 上求一点 P,使最大。 学生 1:对于问题 1,只要过 A 作关于 L 的对称点,再连结交直线 L 于 P 点,即所求。因为两点之间线段最短。对于问题 2,只要连结 AB 并延长交直线 L 于 P 点,即所求。因为三角形任意两边之差小于第三边。教师:看来在一条直线上找一点到两个定点的距离之和最小、距离之差最 大对我们来说很容易,现在看下面的问题。问题 3 若 A(3, 2),F 为抛物线的焦点,在抛物线上找一点 P,使最小及取得最小值时 P 点的坐标。学 生 2 : 过 A 点 作 抛 物 线的 准 线 L 的 垂 线 AD 交 抛 物 线 于 P 点 , 此 时,就是最小的。因为点到直线的所有线中,只有点到直线的距离最短。教师:与问题 1 比较,你发现了什么?学生 3:(3 分钟后)我认为问题 3 与问 题 1 的本质是一样的,都是在线(直线和曲线)找一点到两个定点的距离之和最小。并且解决的方法也一样,问题 3 中的 D 点就“好比”是 F 点关于抛物线(曲线)的“对称”点。如果我们把问题 1 中的直线想象成是拉直的曲线,那问题 1 不就是问题 3 的特殊情况吗?问题 3 不就是问题 1 的推广吗?(全班给予热烈的掌声)变式问题: 已知 A(3,2),F(2,0) ,在双曲线上求一点 P,使其的值最小。学生 4:与问题 3 的解题思路完全一样,只不过,此处要利用双曲线的 定义来作“对LABP图 1LYOXPFDA图 3图 2LPBA称”。(后略)问题 4:已知双曲线,是左焦点,A(-3,-1),在双曲线上求一点 P使的值最小。(2 分钟后)学生 5:此题应作出双曲线的右焦点,连结交双曲线于 P 点,即为 所 求 。 因 为 由 双 曲 线 定 义 知 ,, 即,,此题是利用双曲线定义作的关于双曲线的“对称点”,转化成问题 1 的形式来求解的。教师:你分析得很好!请大家课后去解答完。下面谁来谈谈解决这类问题的收获?学生 6:老师,我...