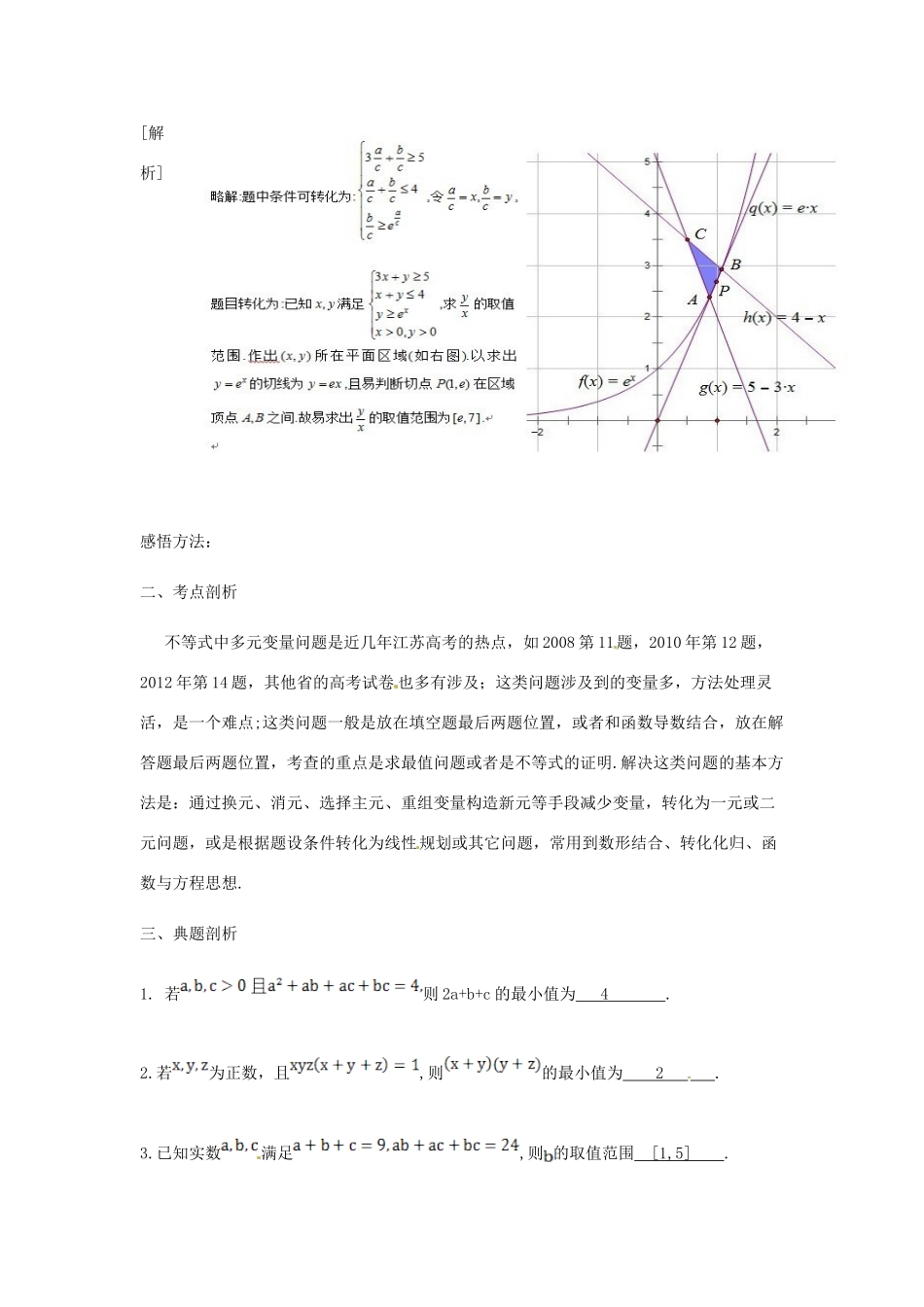
江苏省苏州市第五中学高三数学 不等式中多元变量问题的处理复习学案 一、 真题再现1(2008 江苏卷 11)设为正实数,满足,则的最小值是 3 【解析】本小题考查二元基本不等式的运用.由得,代入得,当且仅当=3 时取“=”.感悟方法:2.(2010 江苏卷 12)设实数 x,y 满足 3≤≤8,4≤≤9,则的最大值是 27 .[解析] ,,,的最大值是 27.感悟方法:3.(2012 江苏 14)已知正数满足:则的取值范围是 .[解析] 感悟方法:二、考点剖析不等式中多元变量问题是近几年江苏高考的热点,如 2008 第 11题,2010 年第 12 题,2012 年第 14 题,其他省的高考试卷 也多有涉及;这类问题涉及到的变量多,方法处理灵活,是一个难点;这类问题一般是放在填空题最后两题位置,或者和函数导数结合,放在解答题最后两题位置,考查的重点是求最值问题或者是不等式的证明.解决这类问题的基本方法是:通过换元、消元、选择主元、重组变量构造新元等手段减少变量,转化为一元或二元问题,或是根据题设条件转化为线性规划或其它问题,常用到数形结合、转化化归、函数与方程思想.三、典题剖析1. 若则 2a+b+c 的最小值为 4 .2.若为正数,且,则的最小值为 2 .3.已知实数满足,则 的取值范围 [1,5] .4.若实数满足,则的最小值为 5.求证:解:是 f(x)=0 的两根2 两式相减得:又, 令则原式=令四、感悟总结:五、巩固提高:1.已知正数满足则的最小值为 .2.已知 .3.已知实数 x,y 满足 则 x+2y 的取值范围为 ] .4.已知实数且,则的最小值 .选编说明:不等式中多元变量问题是近几年江苏高考的热点,如 2008 第 11 题,2010 年第 12 题,2012 年第 14 题,其他省的高考试卷也多有涉及;这类问题涉及到的变量多,方法处理灵活,对学生来说是一个难点;这类问题一般是放在填空题最后两题位置,或和函数导数结合,放在解答题最后两题位置,考查的重点是求最值问题或不等式的证明.解决这类问题的基本方法是:通过换元、消元、选择主元、重组变量构造新元等手段 减少变量,转化为一元或二元问题,或是根据题设条件转化为线性规划或其它问题,常用到数形结合、转化化归、函数与方程思想.通过一轮复习,学生对二元变量求最值问题和利用线性规划或转化为线性规划的问题已基本掌握,因此,此类问题本节课没有涉及.由于处理多变量问题的方法较多,本节课主要围绕减元思想和转化为数形结合选题,前 2 道题都涉及 3 个变量,且式...