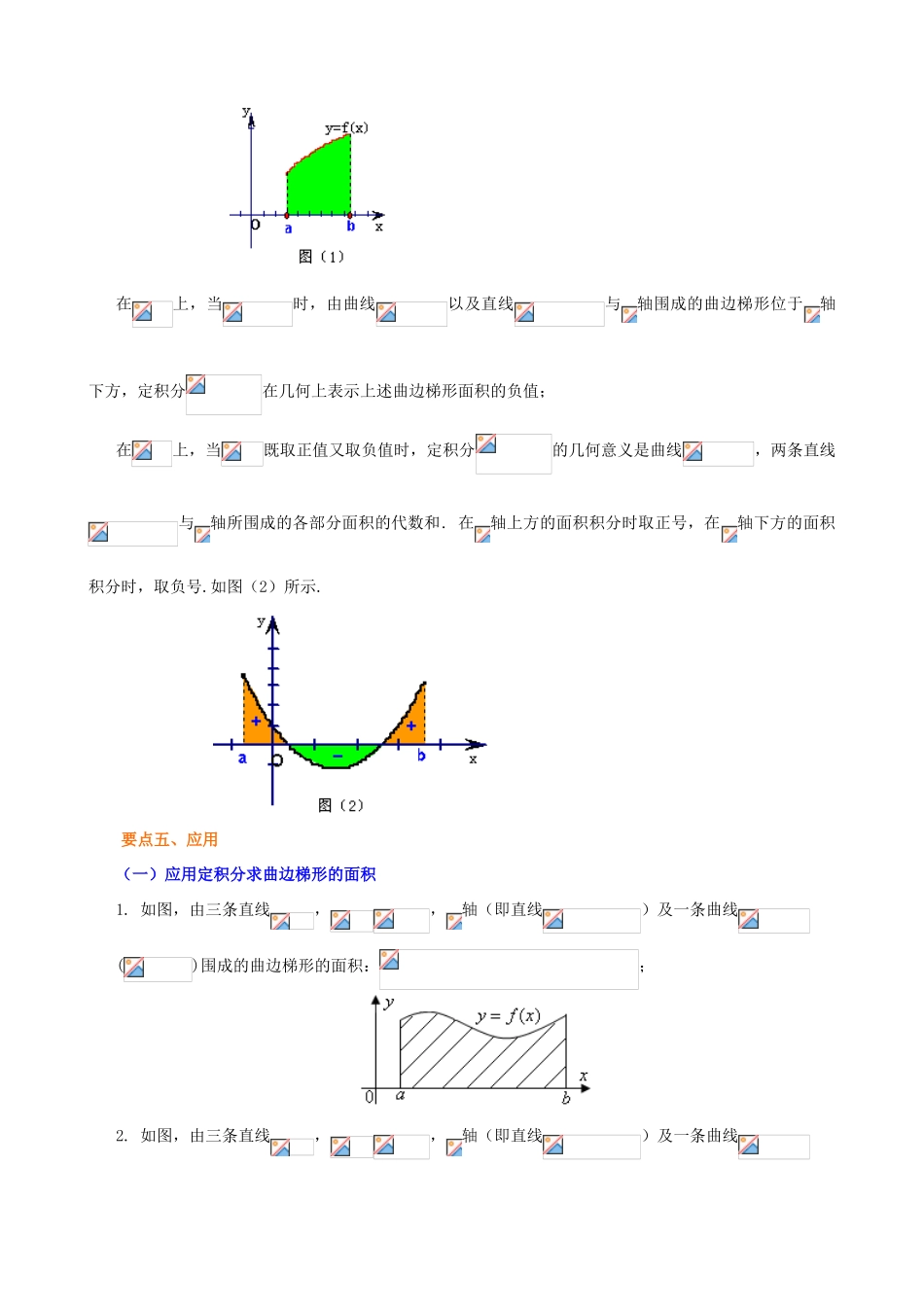
定积分和微积分基本定理【考纲要求】1.了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念及其基本定理。2.正确计算定积分,利用定积分求面积。【知识网络】【考点梳理】要点一、定积分的概念定积分的定义:如果函数在区间上连续,用分点将 区 间等 分 成个 小 区 间 , 在 每 个 小 区 间上 任 取 一 点, 作 和 式,当时,上述和式无限接近某个常数,这个常数叫做函数在区间上的定积分.记作,即=,这里,与分别叫做积分下限与积分上限,区间叫做积分区间,函数叫做被积函数,叫做积分变量,叫做被积式.要点诠释:(1)定积分的值是一个常数,可正、可负、可为零;(2)用定义求定积分的四个基本步骤:①分割;②近似代替;③求和;④取极限.要点二、定积分的性质(1)(为常数),(2),(3)(其中),(4)利用函数的奇偶性求积分: 若函数在区间上是奇函数,则;若函数在区间上是偶函数,则.要点三、微积分基本定理如果,且在上连续,则,其中叫做的一个原函数.由于也是的原函数,其中 c 为常数.一般地,原函数在上的改变量简记作.因此,微积分基本定理可以写成形式:.要点诠释:求定积分主要是要找到被积函数的原函数,也就是说,要找到一个函数,它的导函数等于被积函数 .由此,求导运算与求原函数运算互为逆运算.要点四、定积分的几何意义设函数在区间上连续.在上,当时,定积分在几何上表示由曲线以及直线与轴围成的曲边梯形的面积;如图(1)所示.在上,当时,由曲线以及直线与轴围成的曲边梯形位于轴下方,定积分在几何上表示上述曲边梯形面积的负值;在上,当既取正值又取负值时,定积分的几何意义是曲线,两条直线与轴所围成的各部分面积的代数和. 在轴上方的面积积分时取正号,在轴下方的面积积分时,取负号.如图(2)所示.要点五、应用(一)应用定积分求曲边梯形的面积1. 如图,由三条直线,,轴(即直线)及一条曲线()围成的曲边梯形的面积:;2. 如图,由三条直线,,轴(即直线)及一条曲线()围成的曲边梯形的面积:;3. 如图,由曲线及直线,围成图形的面积公式为:.4.利用定积分求平面图形面积的步骤:(1)画出草图,在直角坐标系中画出曲线或直线的大致图像;(2)借助图形确定出被积函数,求出交点坐标,确定积分的上、下限;(3)写出定积分表达式;(4)求出平面图形的面积.(二)利用定积分解决物理问题① 变速直线运动的路程作变速直线运动的物体所经过的路程,等于其速度...