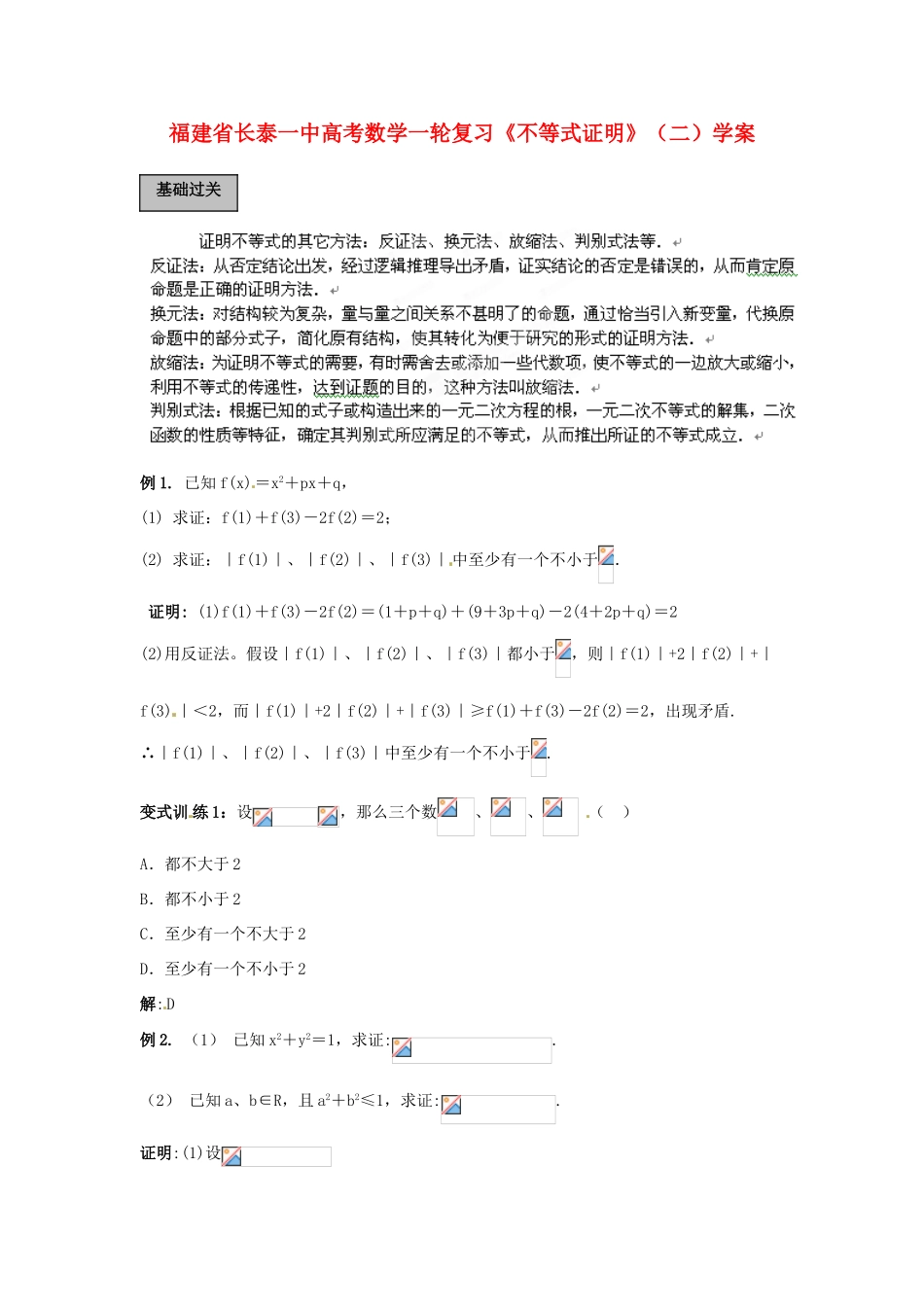
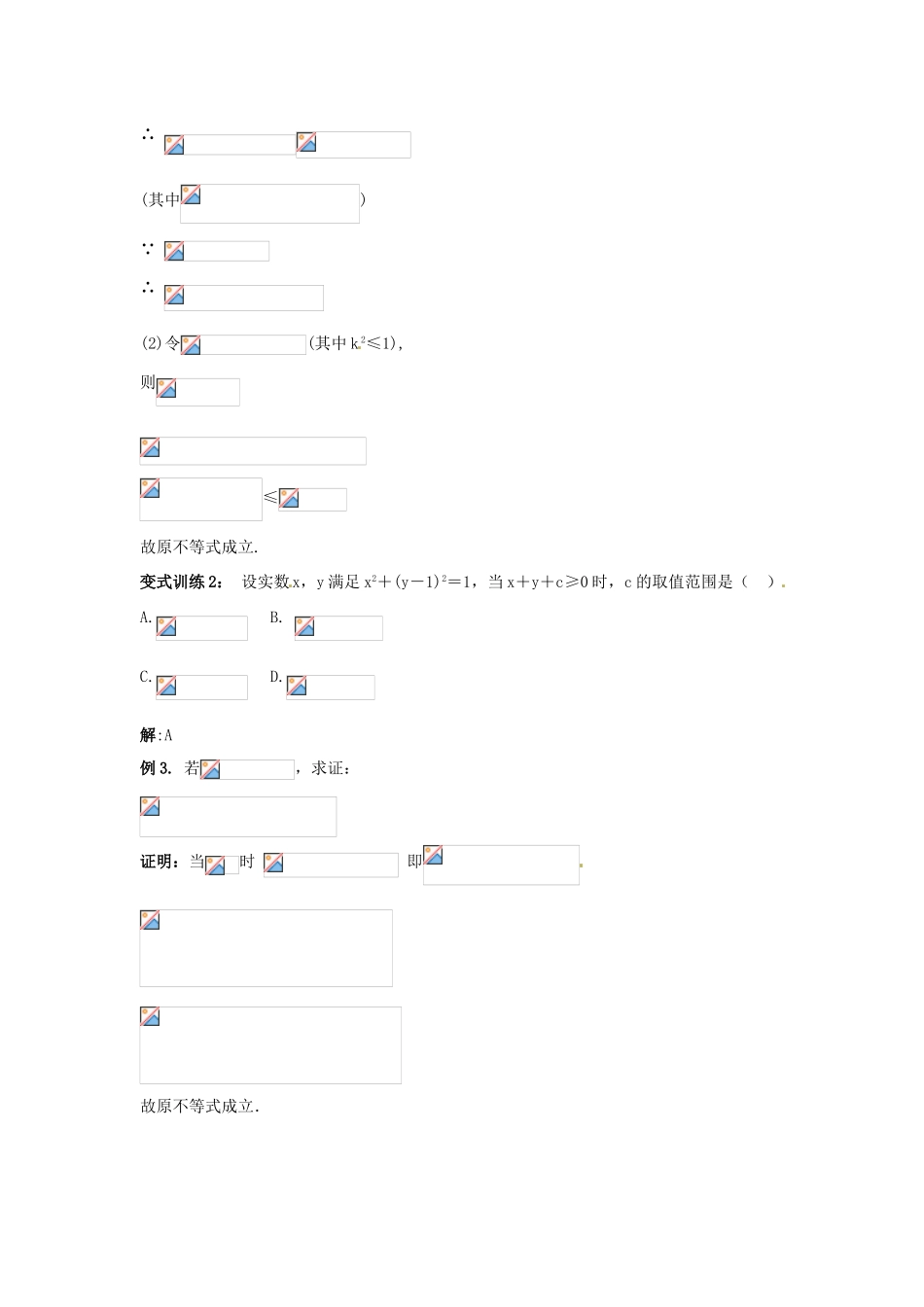
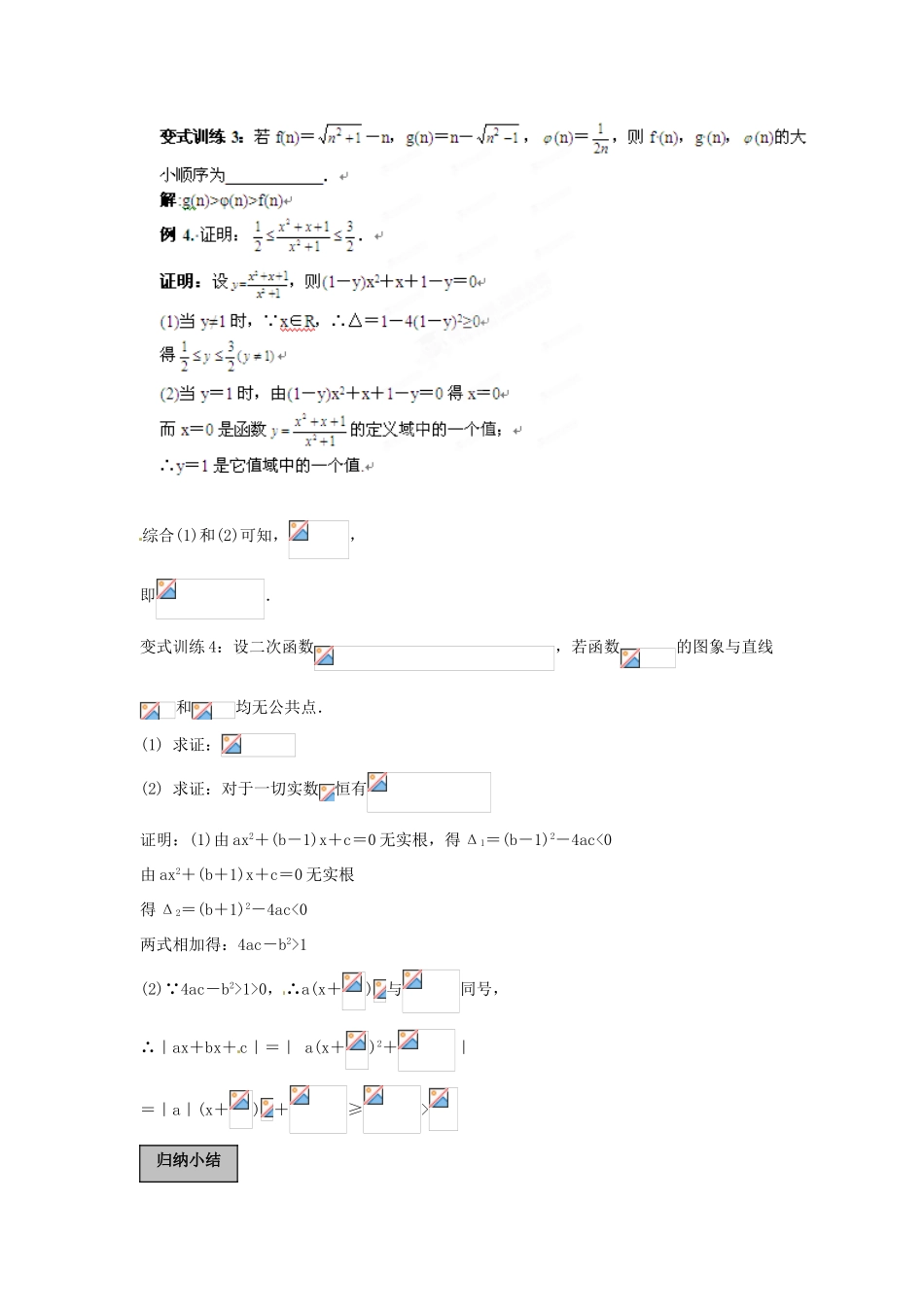
福建省长泰一中高考数学一轮复习《不等式证明》(二)学案例 1. 已知 f(x)=x2+px+q,(1) 求证:f(1)+f(3)-2f(2)=2;(2) 求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于. 证明: (1)f(1)+f(3)-2f(2)=(1+p+q)+(9+3p+q)-2(4+2p+q)=2(2)用反证法。假设|f(1)|、|f(2)|、|f(3)|都小于,则|f(1)|+2|f(2)|+|f(3) |<2,而|f(1)|+2|f(2)|+|f(3)|≥f(1)+f(3)-2f(2)=2,出现矛盾.∴|f(1)|、|f(2)|、|f(3)|中至少有一个不小于.变式训 练 1:设,那么三个数、、 ( )A.都不大于 2B.都不小于 2 C.至少有一个不大于 2 D.至少有一个不小于 2解:D例 2. (1) 已知 x2+y2=1,求证:.(2) 已知 a、b∈R,且 a2+b2≤1,求证:.证明:(1)设基础过关∴ (其中)∵ ∴ (2)令(其中 k 2≤1),则≤故原不等式成立.变式训练 2: 设实数x,y 满足 x2+(y-1)2=1,当 x+y+c≥0 时,c 的取值范围是( )A.B. C.D.解:A例 3. 若,求证:证明:当时 即故原不等式成立.综合(1)和(2)可知,,即.变式训练 4:设二次函数,若函数的图象与直线和均无公共点.(1) 求证:(2) 求证:对于一切实数恒有证明:(1)由 ax2+(b-1)x+c=0 无实根,得 Δ1=(b-1)2-4ac<0由 ax2+(b+1)x+c=0 无实根得 Δ2=(b+1)2-4ac<0两式相加得:4ac-b2>1(2)∵4ac-b2>1>0,∴a(x+) 与同号,∴|ax+bx+c|=| a(x+)2+|=|a|(x+) +≥>归纳小结1.凡是含有“至少”,“至多”,“唯一”,“不存在”或其它否定词的命题适宜用反证法.2.在已知式子中,如果出现两变量之和为正常数或变量的绝对值不大于一个正常数,可进行三角变换,换元法证明不等式时,要注意换元的等价性.3.放缩法证题中,放缩必须有目标,放缩的途径很多,如用均值不等式,增减项、放缩因式等.4.含有字母的不等式,如果可以化成一边为零,另一边是关于某字母的二次三项式时,可用判别式法证明不等式成立,但要注意根的范围和题设条件的限制.