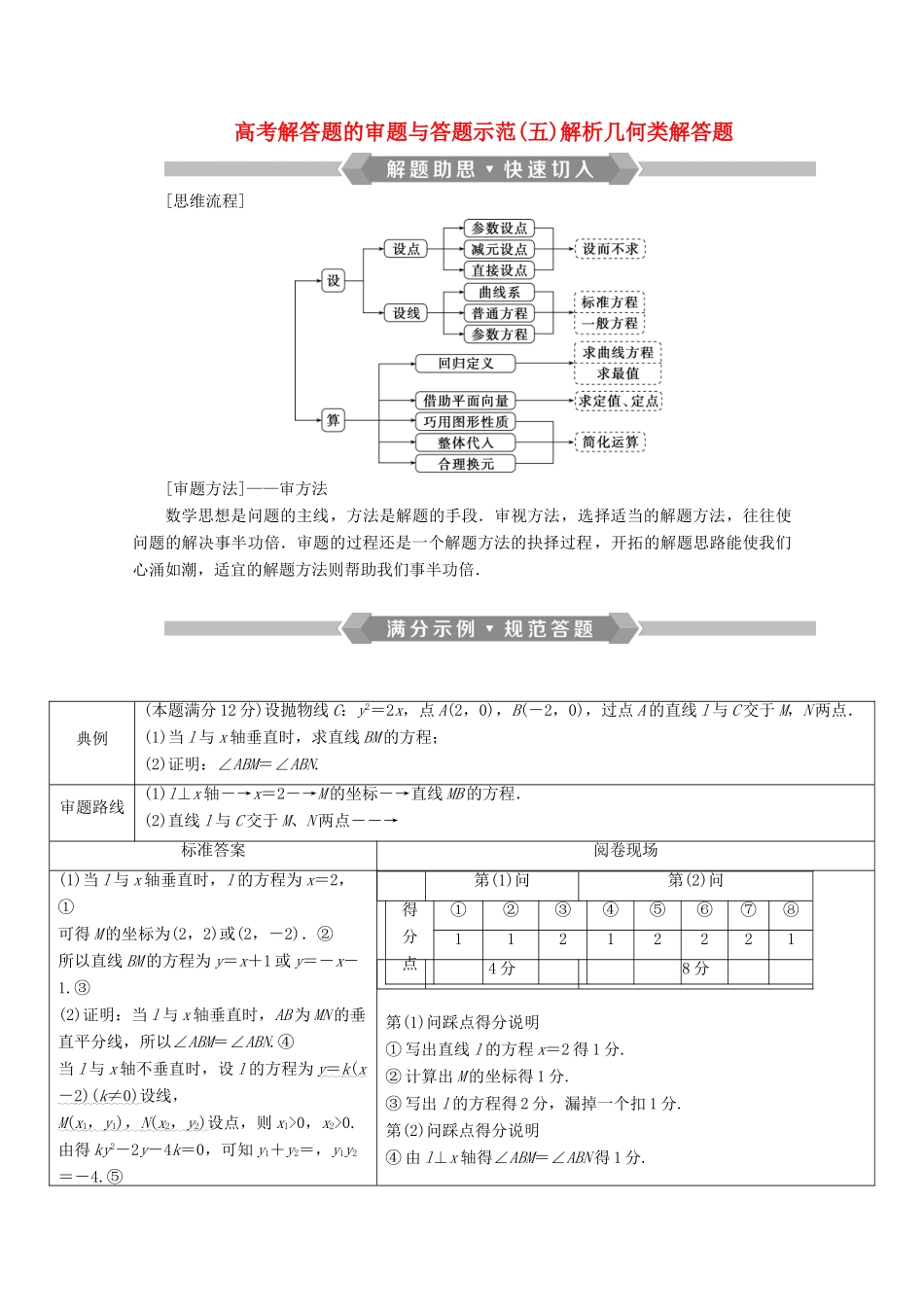
高考解答题的审题与答题示范(五)解析几何类解答题[思维流程][审题方法]——审方法数学思想是问题的主线,方法是解题的手段.审视方法,选择适当的解题方法,往往使问题的解决事半功倍.审题的过程还是一个解题方法的抉择过程,开拓的解题思路能使我们心涌如潮,适宜的解题方法则帮助我们事半功倍.典例(本题满分 12 分)设抛物线 C:y2=2x,点 A(2,0),B(-2,0),过点 A 的直线 l 与 C 交于 M,N 两点.(1)当 l 与 x 轴垂直时,求直线 BM 的方程;(2)证明:∠ABM=∠ABN.审题路线(1)l⊥x 轴―→x=2―→M 的坐标―→直线 MB 的方程.(2)直线 l 与 C 交于 M、N 两点――→标准答案阅卷现场(1)当 l 与 x 轴垂直时,l 的方程为 x=2,①可得 M 的坐标为(2,2)或(2,-2).②所以直线 BM 的方程为 y=x+1 或 y=-x-1.③(2)证明:当 l 与 x 轴垂直时,AB 为 MN 的垂直平分线,所以∠ABM=∠ABN.④当 l 与 x 轴不垂直时,设 l 的方程为 y = k ( x - 2)( k ≠0) 设线,M ( x 1, y 1) , N ( x 2, y 2)设点,则 x1>0,x2>0.由得 ky2-2y-4k=0,可知 y1+y2=,y1y2=-4.⑤第(1)问第(2)问得分点①②③④⑤⑥⑦⑧112122214 分8 分第(1)问踩点得分说明① 写出直线 l 的方程 x=2 得 1 分.② 计算出 M 的坐标得 1 分.③ 写出 l 的方程得 2 分,漏掉一个扣 1 分.第(2)问踩点得分说明④ 由 l⊥x 轴得∠ABM=∠ABN 得 1 分.直线 BM,BN 的斜率之和为kBM+kBN=+=计算.⑥将 x1=+ 2 , x 2=+ 2 及 y 1+ y 2, y 1y2 整体代入的表达式代入上式分子,可得 x2y1+x1y2+2(y1+y2)===0.⑦所以 kBM+kBN=0,可知 BM,BN 的倾斜角互补,所以∠ABM=∠ABN.综上,∠ABM=∠ABN.⑧⑤l 不垂直 x 轴,设出 l 的方程正确运算得 2 分.⑥ 化简 kBM+kBN的代数式得 2 分.⑦ 代入运算 kBM+kBN=0,得 2 分.⑧ 写出结论得 1 分.