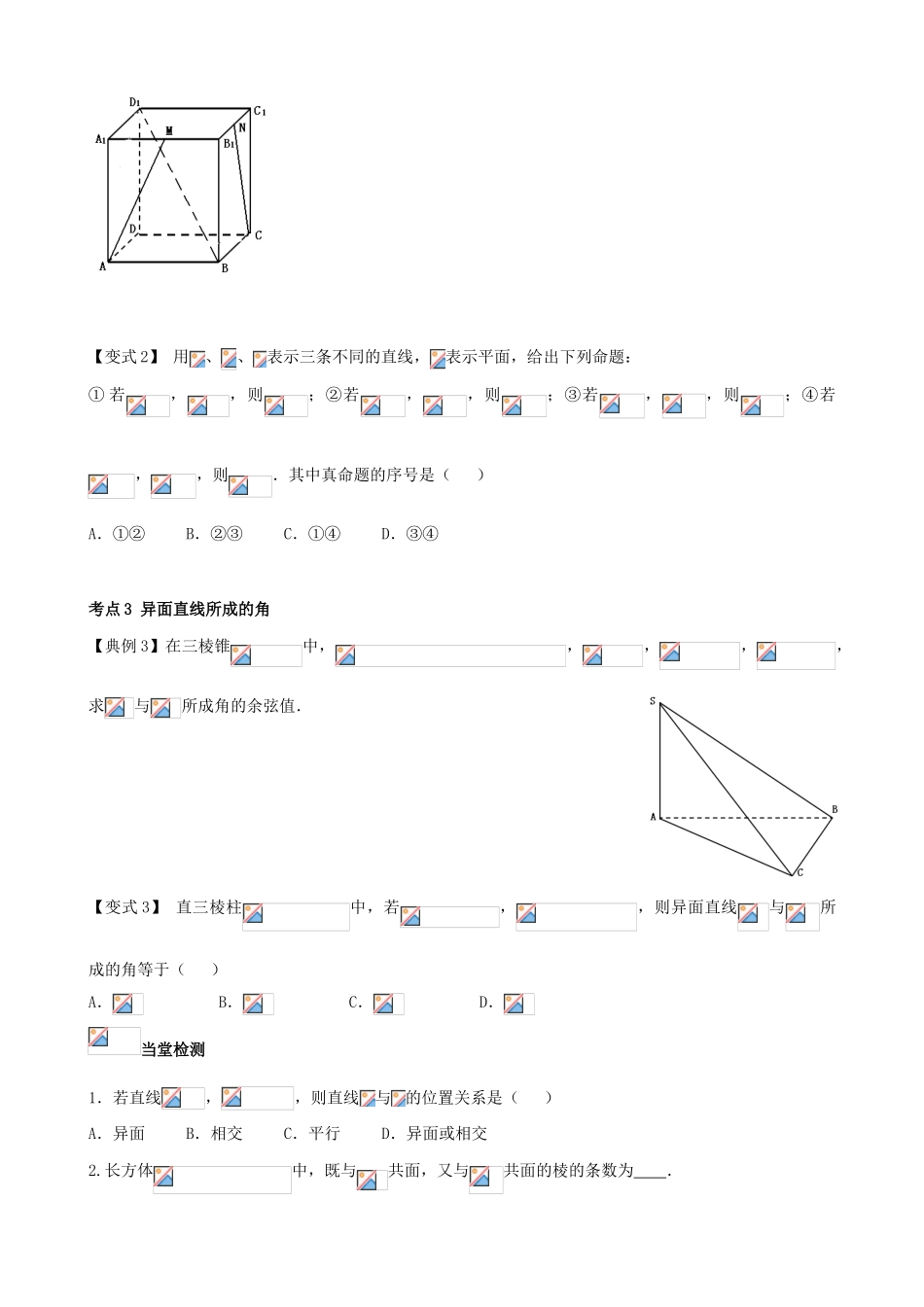
第四十一课时 平面的基本性质 课前预习案考纲要求1.理解空间直线、平面位置关系的定义;2.了解可以作为推理依据的公理和定理.基础知识梳理1.平面的基本性质:公理 1 :如果一条直线上的 在一个平面内,那么这条直线上的所有点都在这个平面内.公理 2:过 的三点,有且只有一个平面.公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有 过该点的公共直线.2.直线与直线的位置关系(1)位置关系的分类: (2)异面直线所成的角① 定义:设,是两条异面直线,经过空间中任一点作直线,,把与所成的 叫做异面直线,所成的角(或夹角).② 范围: .3.直线与平面的位置关系 、 、 三种情况.4.平面与平面的位置关系 、 两种情况.5.平行公理平行于 的两条直线互相平行.6.定理空间中如果两个角的两边分别对应平行,那么这两个角 .预习自测1.已知一个平面, 为空间中的任意一条直线,那么在平面内一定存在直线使得( )A.B. 与相交C. 与是异面直线D.2.已知异面直线,分别在平面,内,且面,则直线与,的位置关系是( )A.与,都相交B.至多与,中的一条相交C.与,都不相交D.至少与,中的一条相交课堂探究案典型例题考点 1 平面的基本性质【典例 1】正方体中,、分别是和的中点.求证:(1)、、、四点共面;(2)、、三线共点.【变式 1】正方体中,、、分别是、、的中点,那么正方体的过、、的截面图形是( )A.三角形B.四边形C.五边形D.六边形考点 2 空间线面的位置关系【典例 2】 如图所示,正方体中,、分别是、的中点.问:(1)和是否是异面直线?说明理由;(2)和是否是异面直线?【变式 2】 用、、表示三条不同的直线,表示平面,给出下列命题:① 若,,则;②若,,则;③若,,则;④若,,则.其中真命题的序号是( )A.①②B.②③C.①④D.③④考点 3 异面直线所成的角【典例 3】在三棱锥中,,,,,求与所成角的余弦值.【变式 3】 直三棱柱中,若,,则异面直线与所成的角等于( )A.B.C.D.当堂检测1.若直线,,则直线与的位置关系是( )A.异面B.相交C.平行D.异面或相交2.长方体中,既与共面,又与共面的棱的条数为 .课后拓展案 A 组全员必做题1.已知,为不重合的两个平面,直线,那么“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.给出下列四个命题:① 垂直于同一直线的两条直线互相...