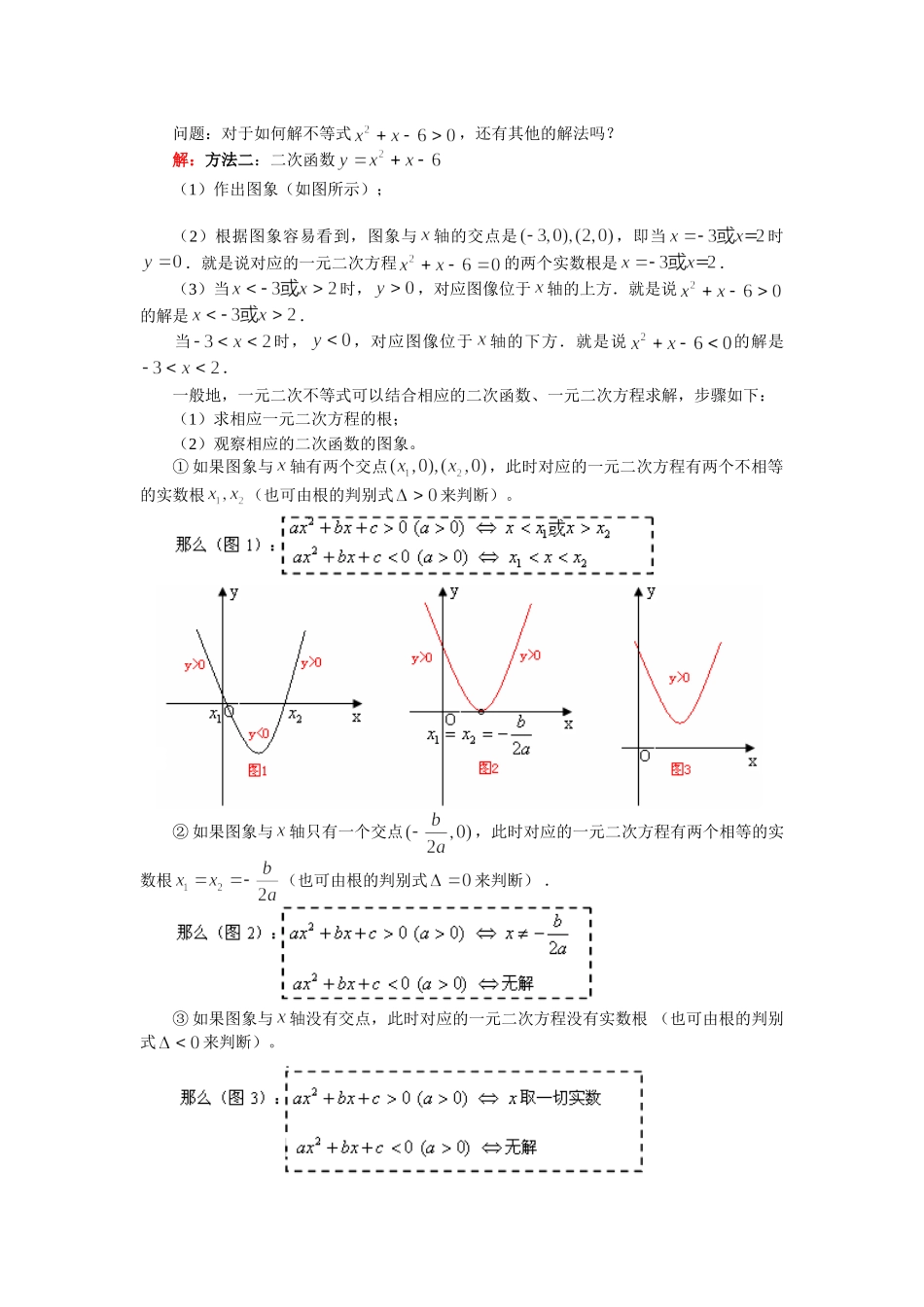
(初升高)高一数学衔接班第5讲——不等式一、学习目标1.掌握一元二次不等式的解法,如不等式组法、图象法2.掌握简单分式不等式的解法3.会解简单的含字母系数的不等式,会求有关字母取值或取值范围的问题二、学习重点一元二次不等式的解法三、课程精讲1.新知探秘问题:如何解不等式.思路导航:不等式左边可以因式分解,根据“符号法则---正正(负负)得正、正负得负”的原则,将其转化为一元一次不等式组.解:方法一:原不等式可以化为:,于是:或所以,原不等式的解是.点津:当把一元二次不等式化为的形式后,只要等式左边可以分解为两个一次因式,即可运用本题的解法。形如的不等式称为关于的一元二次不等式.知识点一:一元二次不等式的解法——不等式组法例1.解下列不等式:(1)(2)思路导航:要先将不等式化为的形式,通常使二次项系数为正数.解:(1)原不等式可化为:,即于是:所以原不等式的解是.(2)原不等式可化为:,即于是:所以原不等式的解是.点津:在将不等式化为的形式时,通常把二次项系数化正,还要注意进行正确的分解因式知识点二:一元二次不等式的解法——图象法问题:对于如何解不等式,还有其他的解法吗?解:方法二:二次函数(1)作出图象(如图所示);(2)根据图象容易看到,图象与轴的交点是,即当时.就是说对应的一元二次方程的两个实数根是.(3)当时,,对应图像位于轴的上方.就是说的解是.当时,,对应图像位于轴的下方.就是说的解是.一般地,一元二次不等式可以结合相应的二次函数、一元二次方程求解,步骤如下:(1)求相应一元二次方程的根;(2)观察相应的二次函数的图象。①如果图象与轴有两个交点,此时对应的一元二次方程有两个不相等的实数根(也可由根的判别式来判断)。②如果图象与轴只有一个交点,此时对应的一元二次方程有两个相等的实数根(也可由根的判别式来判断).③如果图象与轴没有交点,此时对应的一元二次方程没有实数根(也可由根的判别式来判断)。简单的说,求解一元二次不等式的步骤为:(1)求根(2)画图(3)写出解集例2.解下列不等式:(1)(2)思路导航:按着图象法的解题步骤进行解:(1)不等式可化为∴一元二次方程的两根为-2、4∴由图象知,不等式的解是(2)不等式可化为∴由图象知不等式的解是仿练:解:不等式对应的一元二次方程无解由的函数图像可知,原不等式无解点津:实际上,“一元二次方程”、“一元二次函数”“一元二次不等式”之间存在某种内在联系,简称为“三个二次的关系”;“三个二次的关系”完全可以统一到函数的图像中去,即一元二次方程的根是一元二次函数图像与x轴交点的横坐标,也是一元二次不等式解的端点值,当然,这部分内容到高中还会学习到。知识点三:简单分式不等式的解法例3.解下列不等式:(1)(2)思维导航:(1)类似于一元二次不等式的解法,运用“符号法则”将之化为两个一元一次不等式组再进行处理;或者因为两个数(式)相除为异号,那么这两个数(式)相乘也为异号,可将分式不等式直接转化为整式不等式求解.(2)注意到经过配方后,分母实际上是一个正数解:(1)法一:原不等式可化为:法二:原不等式可化为:.(2) 原不等式可化为:点津:分式不等式可以通过转化成一元一次不等式组来求解,当然,还有其他的方法,那就是可以转化成一元二次不等式来求解,但请注意不等式与一元二次不等式是否同解。事实上,它们的解并不相同,的解为,而的解为。例4.解不等式思路导航:分母当中含有未知量x,而不等式的右端并不为0,此题能直接去分母吗?显然,因为分母的符号不能确定,所以此题不能直接去分母,可以通过移项,把不等式的一端化为0。解:原不等式可化为:点津:(1)转化为整式不等式时,一定要先将右端变为0.(2)本例若采取直接去分母的方法,则需要讨论分母的符号:【直击高中】在高中,经常会遇到含有字母系数的不等式,这样的字母我们称为参数,在含有参数的不等式中,由于参数取值的不同,会导致不等式解的不确定,换句话说,参数取值的不同,导致不等式解的结果不同,所以往往需要对参数的取值范围分情况讨论,从而讨论不等式的解...