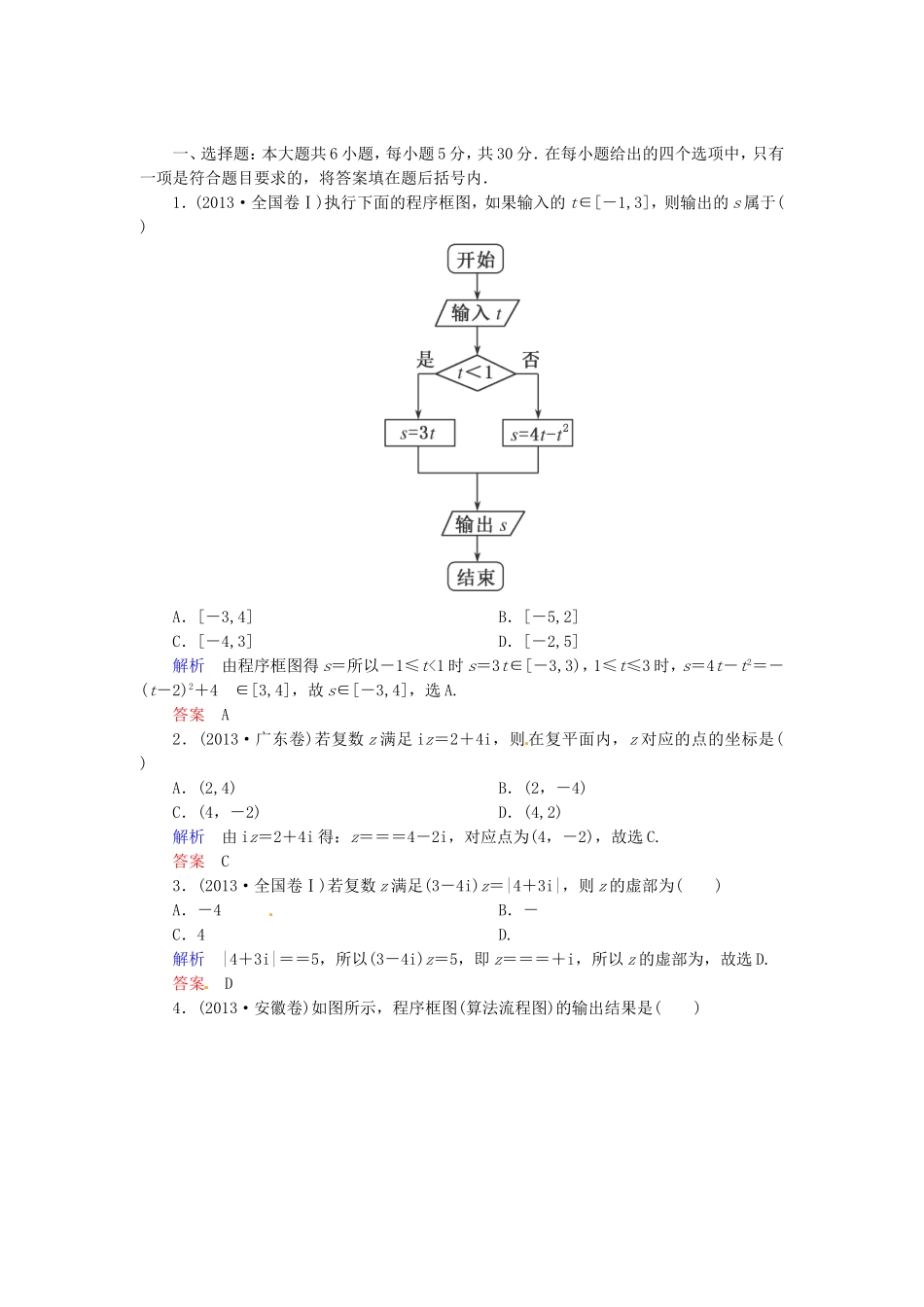
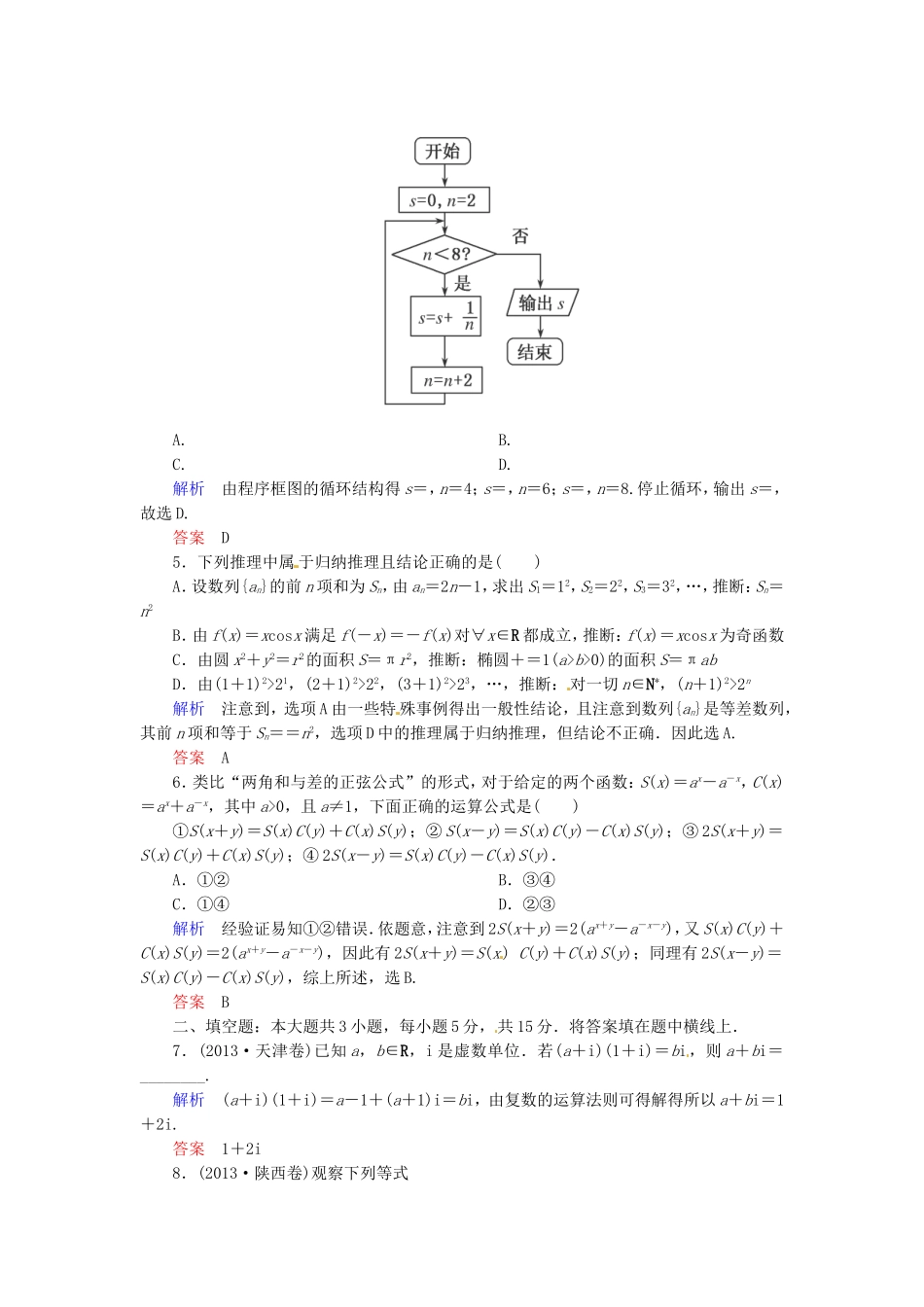
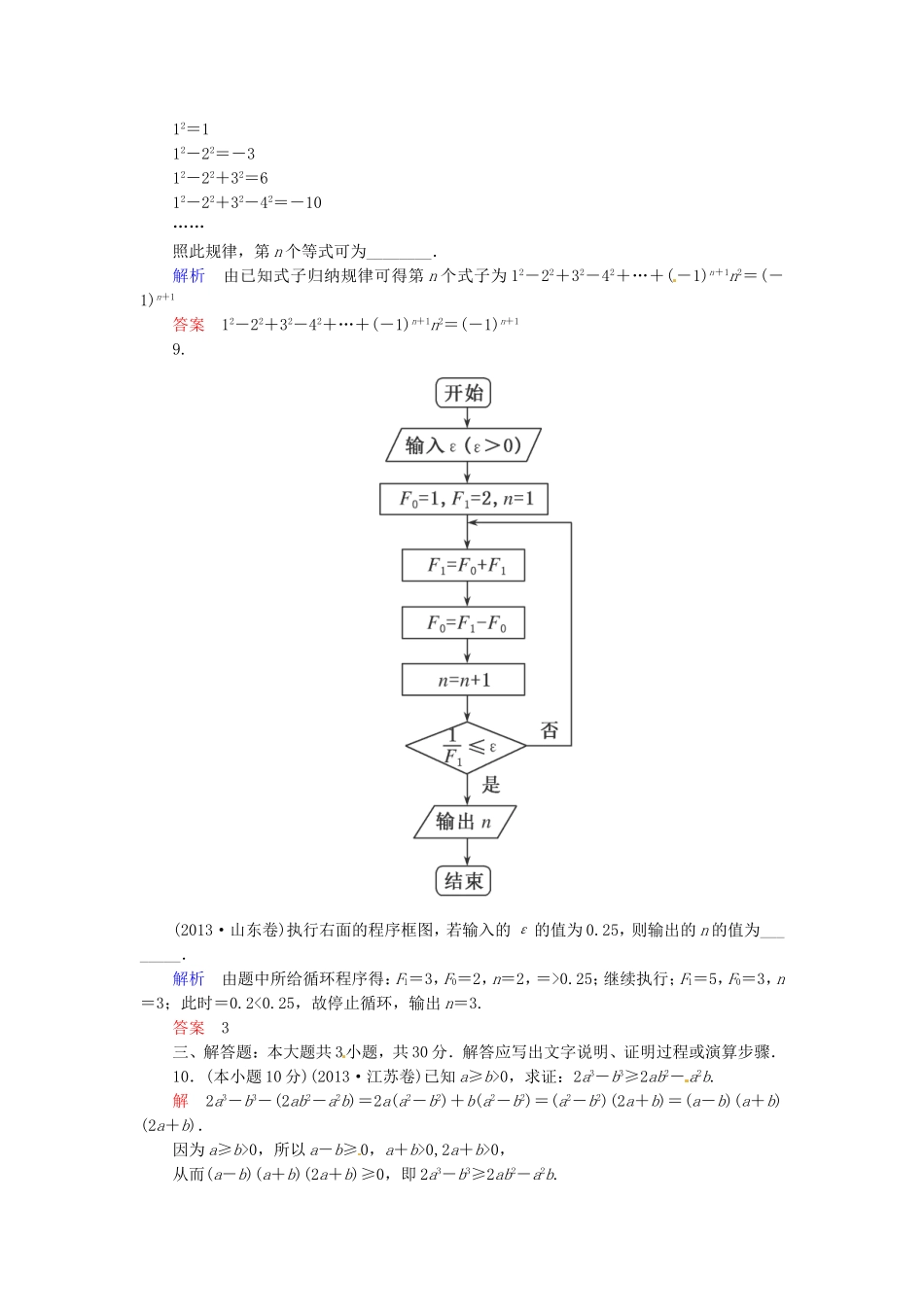
一、选择题:本大题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在题后括号内.1.(2013·全国卷Ⅰ)执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于()A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]解析由程序框图得s=所以-1≤t<1时s=3t∈[-3,3),1≤t≤3时,s=4t-t2=-(t-2)2+4∈[3,4],故s∈[-3,4],选A.答案A2.(2013·广东卷)若复数z满足iz=2+4i,则在复平面内,z对应的点的坐标是()A.(2,4)B.(2,-4)C.(4,-2)D.(4,2)解析由iz=2+4i得:z===4-2i,对应点为(4,-2),故选C.答案C3.(2013·全国卷Ⅰ)若复数z满足(3-4i)z=|4+3i|,则z的虚部为()A.-4B.-C.4D.解析|4+3i|==5,所以(3-4i)z=5,即z===+i,所以z的虚部为,故选D.答案D4.(2013·安徽卷)如图所示,程序框图(算法流程图)的输出结果是()A.B.C.D.解析由程序框图的循环结构得s=,n=4;s=,n=6;s=,n=8.停止循环,输出s=,故选D.答案D5.下列推理中属于归纳推理且结论正确的是()A.设数列{an}的前n项和为Sn,由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2B.由f(x)=xcosx满足f(-x)=-f(x)对∀x∈R都成立,推断:f(x)=xcosx为奇函数C.由圆x2+y2=r2的面积S=πr2,推断:椭圆+=1(a>b>0)的面积S=πabD.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n解析注意到,选项A由一些特殊事例得出一般性结论,且注意到数列{an}是等差数列,其前n项和等于Sn==n2,选项D中的推理属于归纳推理,但结论不正确.因此选A.答案A6.类比“两角和与差的正弦公式”的形式,对于给定的两个函数:S(x)=ax-a-x,C(x)=ax+a-x,其中a>0,且a≠1,下面正确的运算公式是()①S(x+y)=S(x)C(y)+C(x)S(y);②S(x-y)=S(x)C(y)-C(x)S(y);③2S(x+y)=S(x)C(y)+C(x)S(y);④2S(x-y)=S(x)C(y)-C(x)S(y).A.①②B.③④C.①④D.②③解析经验证易知①②错误.依题意,注意到2S(x+y)=2(ax+y-a-x-y),又S(x)C(y)+C(x)S(y)=2(ax+y-a-x-y),因此有2S(x+y)=S(x)C(y)+C(x)S(y);同理有2S(x-y)=S(x)C(y)-C(x)S(y),综上所述,选B.答案B二、填空题:本大题共3小题,每小题5分,共15分.将答案填在题中横线上.7.(2013·天津卷)已知a,b∈R,i是虚数单位.若(a+i)(1+i)=bi,则a+bi=________.解析(a+i)(1+i)=a-1+(a+1)i=bi,由复数的运算法则可得解得所以a+bi=1+2i.答案1+2i8.(2013·陕西卷)观察下列等式12=112-22=-312-22+32=612-22+32-42=-10……照此规律,第n个等式可为________.解析由已知式子归纳规律可得第n个式子为12-22+32-42+…+(-1)n+1n2=(-1)n+1答案12-22+32-42+…+(-1)n+1n2=(-1)n+19.(2013·山东卷)执行右面的程序框图,若输入的ε的值为0.25,则输出的n的值为________.解析由题中所给循环程序得:F1=3,F0=2,n=2,=>0.25;继续执行;F1=5,F0=3,n=3;此时=0.2<0.25,故停止循环,输出n=3.答案3三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.10.(本小题10分)(2013·江苏卷)已知a≥b>0,求证:2a3-b3≥2ab2-a2b.解2a3-b3-(2ab2-a2b)=2a(a2-b2)+b(a2-b2)=(a2-b2)(2a+b)=(a-b)(a+b)(2a+b).因为a≥b>0,所以a-b≥0,a+b>0,2a+b>0,从而(a-b)(a+b)(2a+b)≥0,即2a3-b3≥2ab2-a2b.11.(本小题10分)已知数列{an}中,a1=5且an=2an-1+2n-1(n≥2且n∈N*).(1)证明:数列为等差数列;(2)求数列{an}的前n项和Sn.解(1)设bn=,则b1==2.因为bn+1-bn=-=[(an+1-2an)+1]=[(2n+1-1)+1]=1,所以数列为首项是2,公差是1的等差数列.(2)由(1)知,=+(n-1)×1,∴an=(n+1)·2n+1. Sn=(2·21+1)+(3·22+1)+…+(n·2n-1+1)+[(n+1)·2n+1],∴Sn=2·21+3·22+…+n·2n-1+(n+1)·2n+n.设Tn=2·21+3·22+…+n·2n-1+(n+1)·2n,①2Tn=2·22+3·23+…+n·2n+(n+1)·2n+1.②②-①,得Tn=-2·21...