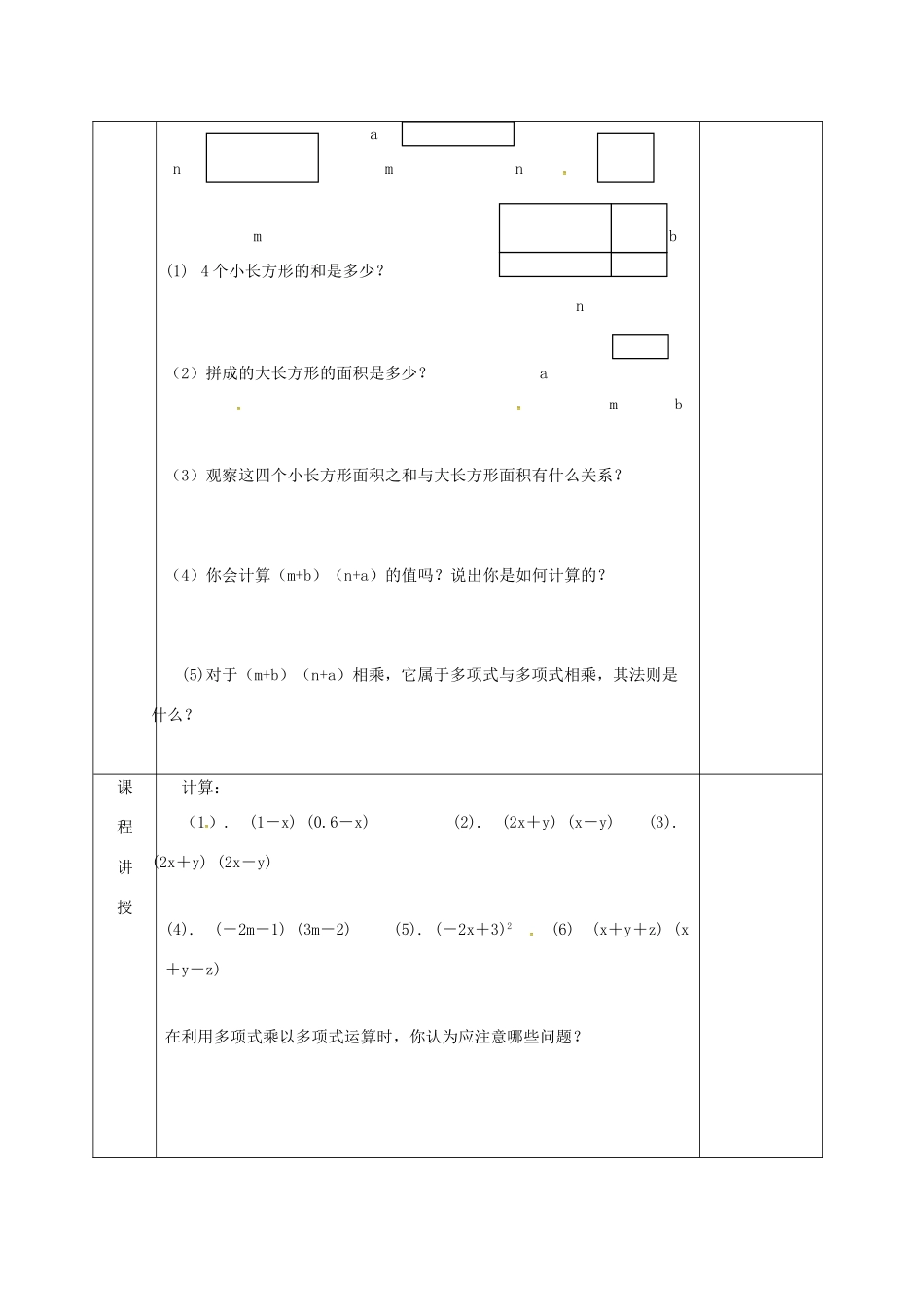
整式的乘法课题1.4.3整式的乘法(3)课型新授课教学目标经历探索整式乘法运算法则的过程,会进行多项式与多项式的乘法运算。重点多项式的乘法法则难点多项式相乘的依据。。教学用具教学环节说明二次备课复习活动内容:复习已学过的运算性质(1)(-2.5x3)(-4xy2)=(),(-2x2y)2(-xyz)=(),(2×103)(8×108)=()(2)-a(2a2+3a-1)=(),-6x(x-3y)=(),(x2y-6xy)×(xy2)=(),3ab×(a2+ab)=(),(x2-x+1)×(-x2)=()新课导入探究活动:将一个长为x,宽为y的长方形的长增加m,得到的新长方形的面积是多少?如图所示,有四个大小不同的小长方形,拼成一个大长方形。anmnambb(1)4个小长方形的和是多少?n(2)拼成的大长方形的面积是多少?amb(3)观察这四个小长方形面积之和与大长方形面积有什么关系?(4)你会计算(m+b)(n+a)的值吗?说出你是如何计算的?(5)对于(m+b)(n+a)相乘,它属于多项式与多项式相乘,其法则是什么?课程讲授计算:(1).(1-x)(0.6-x)(2).(2x+y)(x-y)(3).(2x+y)(2x-y)(4).(-2m-1)(3m-2)(5).(-2x+3)2(6)(x+y+z)(x+y-z)在利用多项式乘以多项式运算时,你认为应注意哪些问题?创新探究:计算下列各式的结果,请观察,比较所得的结果有什么异同,总结规律后,请直接计算:(x+2)(x+3);(x-2)(x-3);(x+2)(x-3);(x-2)(x-3)(1)(x+1)(x+4)=x2+x+(2)(x+4)(x-5)=x2+x+(3)(x-3)(x-4)=x2+x+(4)(x+6)(x-1)=x2+x+总结规律:。小结师生互相交流本堂课上应该掌握的多项式乘法法则,教师对课堂上发现的学生掌握不好的地方给以强调.特别要注意已经学习过的单项式与多项式乘法法则,它们之间的联系与区别也是这堂课要掌握的。作业布置板书设计课后反思