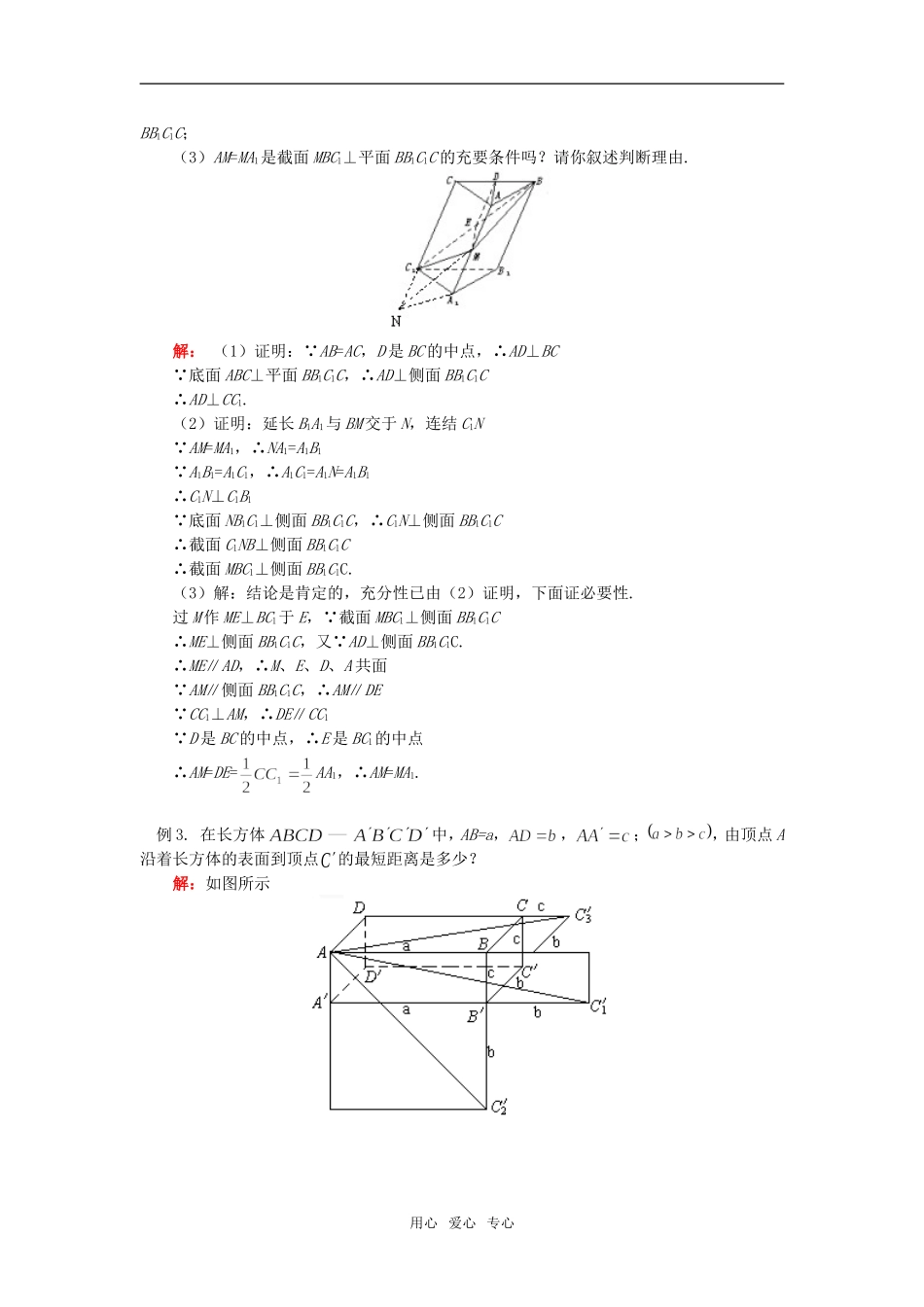
高三数学第二轮专题复习五立体几何(文)人教实验版(B)【本讲教育信息】一.教学内容:高三数学第二轮专题复习五立体几何二、高考要求(1)空间几何体①认识柱、锥、台、球及其简单几何体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.②能画出简单几何空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图表示的立体模型,会用斜二测画法画出它们的直观图.③会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.④会画出某些建筑物的三视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).⑤了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).(2)点、直线、平面之间的位置关系①理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.◆公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内.◆公理2:过不在同一条直线上的三点,有且只有一个平面.◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.◆公理4:平行于同一条直线的两条直线互相平行.◆定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.②以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理.理解以下判定定理:◆如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.理解以下性质定理,并能够证明:◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.◆垂直于同一个平面的两条直线平行.◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.③能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.三、考点聚焦考点1:柱、锥、台、球的体积与面积的计算;考点2:三视图的关系与画法;斜二测直观图;用心爱心专心考点3:简单几何体中的线面关系证明;考点4:正三、四、五棱柱、锥、台的特征量之间的关系。考点5:空间元素点、线、面之间的垂直与平行关系的判断;考点6:空间线面垂直与平行关系的证明;简单几何体中的线面关系证明;四、热点预测2007年新课标立体几何的客观题考查的主要内容是空间的点、线、面的位置关系及三视图与直观图、空间几何体的表面积和体积,考查了考生通过直观感知、操作确认、思维辩证、度量计算等方法认识和探索几何图形及其性质的基本方法,预测2008年高考对该专题的考查应将以棱柱、棱锥为背景,考查线面的位置关系、三视图与几何体的体积与表面积相结合的题目。【典型例题】例1.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE.证一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB.∴MP∥NQ,又AM=NF,AC=BF,∴MC=NB,∠MCP=∠NBQ=45°∴Rt△MCP≌Rt△NBQ∴MP=NQ,故四边形MPQN为平行四边形∴MN∥PQ PQ平面BCE,MN在平面BCE外,∴MN∥平面BCE.证二:如图过M作MH⊥AB于H,则MH∥BC,∴连结NH,由BF=AC,FN=AM,得,由∴MN∥平面BCE.例2.在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.(1)若D是BC的中点,求证:AD⊥CC1;(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面用心爱心专心BB1C1C;(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由.解:(1)证明: AB=AC,D是BC的中点,∴AD⊥BC 底面ABC⊥平面BB1C1C,∴AD⊥侧面BB1C1C∴AD⊥CC1.(2)证明:延长B1A1与BM交于N,连结C1N AM=MA1,∴NA1=A1B1 A1B1=A1C1,∴A1C1=A1N=A1B1∴C1N⊥C1B1 底面NB1C1⊥侧面BB1C1C,∴C1N⊥侧面BB1...