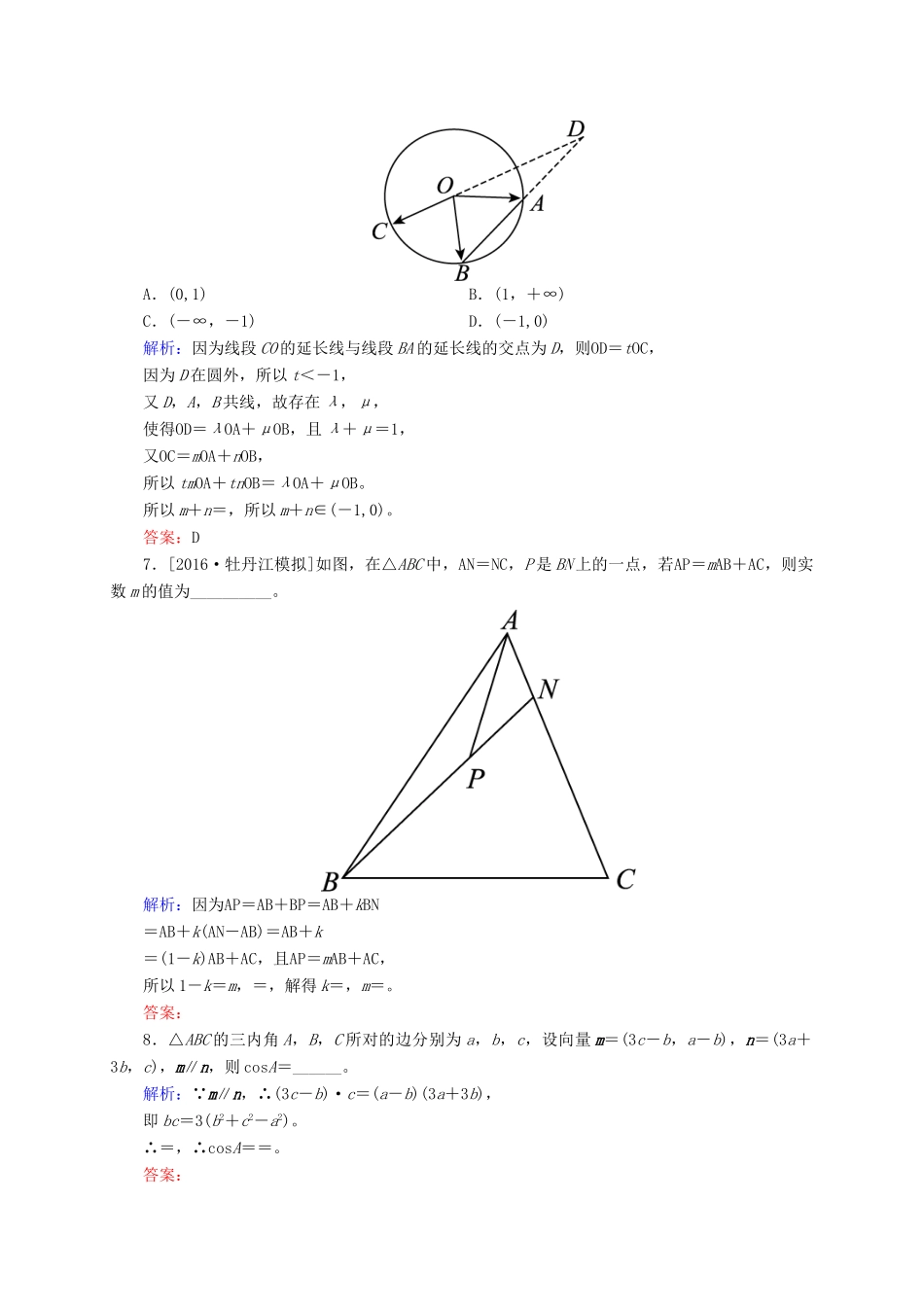
开卷速查(二十五)平面向量基本定理及坐标表示A级基础巩固练1.已知向量a=(2,4),b=(-1,1),则2a-b=()A.(5,7)B.(5,9)C.(3,7)D.(3,9)解析:因为a=(2,4),b=(-1,1),所以2a-b=(2×2-(-1),2×4-1)=(5,7),选A。答案:A2.[2016·广州模拟]若向量BA=(2,3),CA=(4,7),则BC等于()A.(-2,-4)B.(2,4)C.(6,10)D.(-6,-10)解析:因为CA=(4,7),所以AC=(-4,-7)。又BC=BA+AC=(2,3)+(-4,-7)=(-2,-4),故BC=(-2,-4)。答案:A3.[2016·丽江模拟]已知向量a=(1,-2),b=(m,4),且a∥b,则2a-b=()A.(4,0)B.(0,4)C.(4,-8)D.(-4,8)解析:因为向量a=(1,-2),b=(m,4),且a∥b,所以1×4+2m=0,即m=-2,2a-b=2×(1,-2)-(-2,4)=(4,-8)。答案:C4.[2016·兰州模拟]已知D为△ABC的边AB的中点M在DC上且满足5AM=AB+3AC,则△ABM与△ABC的面积比为()A.B.C.D.解析:由5AM=AB+3AC得2AM=2AD+3MC,即2(AM-AD)=3(AC-AM),即2DM=3MC,所以DM=DC,所以△ABM与△ABC同底且高的比为3∶5,所以S△ABM∶S△ABC=3∶5,故选C。答案:C5.[2016·芜湖模拟]在△ABC中,已知a,b,c分别为角A,B,C所对的边,S为△ABC的面积,若向量p=(4,a2+b2-c2),q=(1,S)满足p∥q,则∠C=()A.B.C.D.解析:因为向量p=(4,a2+b2-c2),q=(1,S)满足p∥q,所以a2+b2-c2-4S=0,即4S=a2+b2-c2,则4×absinC=a2+b2-c2,即sinC==cosC,则tanC=1,解得C=。故选A。答案:A6.[2016·临沂模拟]如图所示,A,B,C是⊙O上的三点,线段CO的延长线与线段BA的延长线交于⊙O外的一点D,若OC=mOA+nOB,则m+n的取值范围是()A.(0,1)B.(1,+∞)C.(-∞,-1)D.(-1,0)解析:因为线段CO的延长线与线段BA的延长线的交点为D,则OD=tOC,因为D在圆外,所以t<-1,又D,A,B共线,故存在λ,μ,使得OD=λOA+μOB,且λ+μ=1,又OC=mOA+nOB,所以tmOA+tnOB=λOA+μOB。所以m+n=,所以m+n∈(-1,0)。答案:D7.[2016·牡丹江模拟]如图,在△ABC中,AN=NC,P是BN上的一点,若AP=mAB+AC,则实数m的值为__________。解析:因为AP=AB+BP=AB+kBN=AB+k(AN-AB)=AB+k=(1-k)AB+AC,且AP=mAB+AC,所以1-k=m,=,解得k=,m=。答案:8.△ABC的三内角A,B,C所对的边分别为a,b,c,设向量m=(3c-b,a-b),n=(3a+3b,c),m∥n,则cosA=______。解析: m∥n,∴(3c-b)·c=(a-b)(3a+3b),即bc=3(b2+c2-a2)。∴=,∴cosA==。答案:9.已知向量a=(2,3),b=(-1,2),若ma+nb与a-2b共线,则=______。解析:ma+nb=(2m,3m)+(-n,2n)=(2m-n,3m+2n),a-2b=(2,3)-(-2,4)=(4,-1)。由于ma+nb与a-2b共线,则有=,∴n-2m=12m+8n,∴=-。答案:-10.已知a=(1,0),b=(2,1)。求:(1)|a+3b|;(2)当k为何实数时,ka-b与a+3b平行,平行时它们是同向还是反向?解析:(1) a=(1,0),b=(2,1),∴a+3b=(7,3),故|a+3b|==。(2)ka-b=(k-2,-1),a+3b=(7,3)。 ka-b与a+3b平行,∴3(k-2)+7=0,即k=-。此时ka-b=(k-2,-1)=,a+3b=(7,3),则a+3b=-3(ka-b),即此时向量a+3b与ka-b方向相反。B级能力提升练11.设OA=(1,-2),OB=(a,-1),OC=(-b,0),a>0,b>0,O为坐标原点,若A,B,C三点共线,则+的最小值为__________。解析:AB=OB-OA=(a-1,1),AC=OC-OA=(-b-1,2)。 A,B,C三点共线,∴AB∥AC。∴2(a-1)-(-b-1)=0,∴2a+b=1。∴+=(2a+b)=4++≥4+2=8。当且仅当=,即b=,a=时取等号。∴+的最小值是8。答案:812.在平面直角坐标系中,O为坐标原点,已知向量a=(2,1),A(1,0),B(cosθ,t)。(1)若a∥AB,且|AB|=|OA|,求向量OB的坐标;(2)若a∥AB,求y=cos2θ-cosθ+t2的最小值。解析:(1) AB=(cosθ-1,t),又a∥AB,∴2t-cosθ+1=0。∴cosθ-1=2t。①又 |AB|=|OA|,∴(cosθ-1)2+t2=5。②由①②得,5t2=5,∴t2=1。∴t=±1。当t=1时,cosθ=3(舍去),当t=-1时,cosθ=-1,∴B(-1,-1),...