第七章 第七节 用向量解决平行、垂直及夹角的计算VIP免费

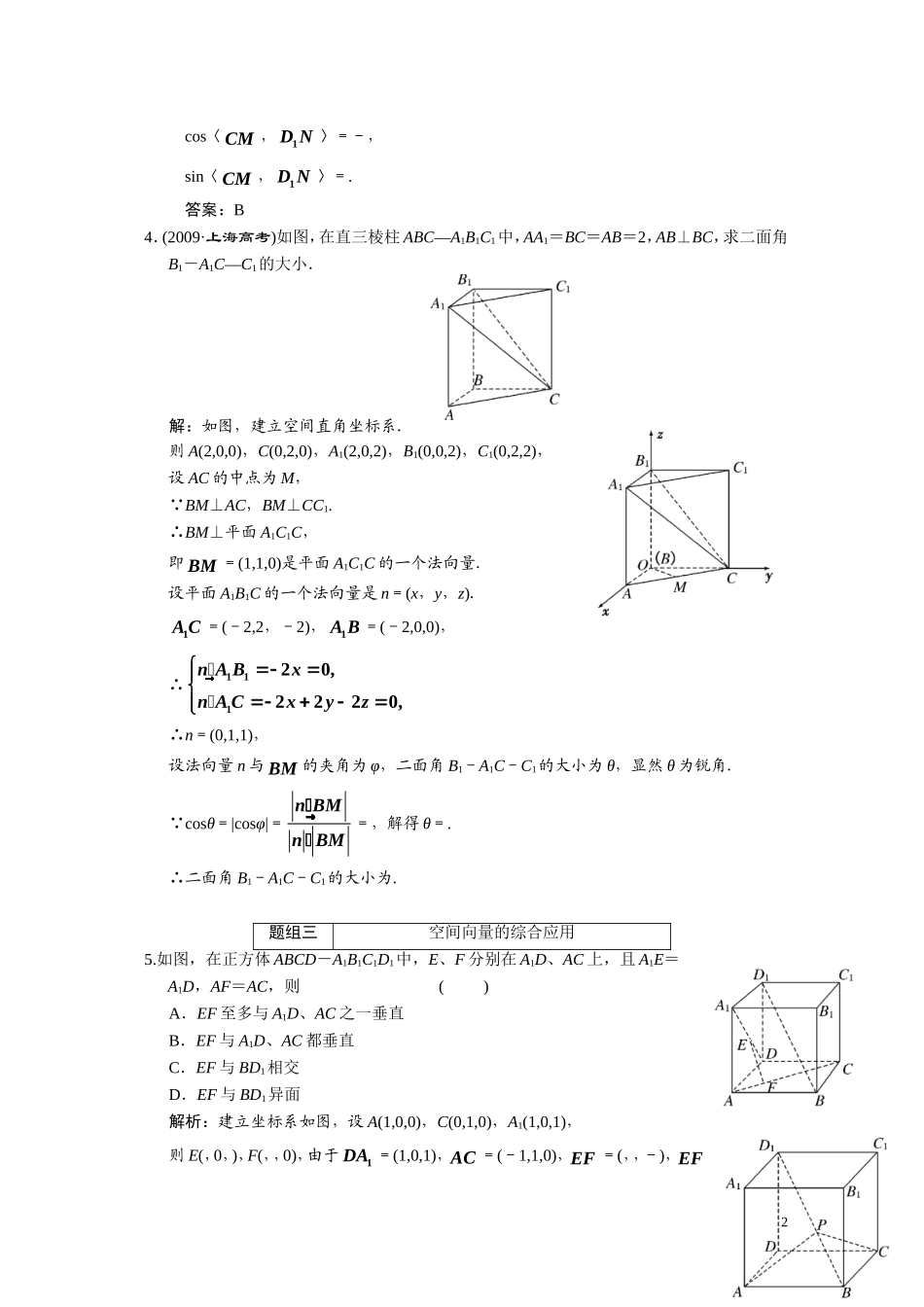
第七章第七节用向量解决平行、垂直及夹角的计算（理）题组一利用空间向量证明平行、垂直问题1.在正方体ABCD－A1B1C1D1中，若E为A1C1中点，则直线CE垂直于()A．ACB．BDC．A1DD．A1A解析：如图所示，易证BD⊥平面AA1C1C，又CE平面ACC1A1，∴BD⊥CE.答案：B2．如图，在正方体ABCD－A1B1C1D1中，棱长为a，M、N分别为A1B和AC上的点，A1M＝AN＝，则MN与平面BB1C1C的位置关系是()A．相交B．平行C．垂直D．不能确定解析： 正方体棱长为a，A1M＝AN＝，∴MB�＝1AB�，CN�＝CA�，∴MN�＝MB�＋BC�＋CN�＝1AB�＋BC�＋CA�＝(11AB�＋1BB�)＋BC�＋(CD�＋DA�)＝1BB�＋11BC�.又 CD�是平面B1BCC1的法向量，且MN�·CD�＝(1BB�＋11BC�)·CD�＝0，∴MN�⊥CD�，∴MN∥平面B1BCC1.答案：B题组二利用空间向量求空间角3.在正方体ABCD－A1B1C1D1中，M、N分别为棱AA1和BB1的中点，则sin〈CM�，1DN�〉的值为()A.B.C.D.解析：设正方体棱长为2，以D为坐标原点，DA为x轴，DC为y轴，DD1为z轴建立空间直角坐标系，可知CM�＝(2，－2,1)，1DN�＝(2,2，－1)，1cos〈CM�，1DN�〉＝－，sin〈CM�，1DN�〉＝.答案：B4．(2009·上海高考)如图，在直三棱柱ABC—A1B1C1中，AA1＝BC＝AB＝2，AB⊥BC，求二面角B1－A1C—C1的大小．解：如图，建立空间直角坐标系．则A(2,0,0)，C(0,2,0)，A1(2,0,2)，B1(0,0,2)，C1(0,2,2)，设AC的中点为M， BM⊥AC，BM⊥CC1.∴BM⊥平面A1C1C，即BM�＝(1,1,0)是平面A1C1C的一个法向量．设平面A1B1C的一个法向量是n＝(x，y，z)．1AC�＝(－2,2，－2)，1AB�＝(－2,0,0)，∴11120,2220,nABxnACxyz��∴n＝(0,1,1)，设法向量n与BM�的夹角为φ，二面角B1－A1C－C1的大小为θ，显然θ为锐角． cosθ＝|cosφ|＝nBMnBM��＝，解得θ＝.∴二面角B1－A1C－C1的大小为.题组三空间向量的综合应用5.如图，在正方体ABCD－A1B1C1D1中，E、F分别在A1D、AC上，且A1E＝A1D，AF＝AC，则()A．EF至多与A1D、AC之一垂直B．EF与A1D、AC都垂直C．EF与BD1相交D．EF与BD1异面解析：建立坐标系如图，设A(1,0,0)，C(0,1,0)，A1(1,0,1)，则E(，0，)，F(，，0)，由于1DA�＝(1,0,1)，AC�＝(－1,1,0)，EF�＝(，，－)，EF�2·1DA�＝0，EF�·AC�＝0，EF与A1D，AC都垂直．答案：B6．如图，设动点P在棱长为1的正方体ABCD－A1B1C1D1的对角线BD1上，记＝λ.当∠APC为钝角时，求λ的取值范围．解：由题设可知，以DA�、DC�、1DD�为单位正交基底，建立如图所示的空间直角坐标系D－xyz，则有A(1,0,0)，B(1,1,0)，C(0,1,0)，D1(0,0,1)．由1DB�＝(1,1，－1)，得1DP�＝λ1DB�＝(λ，λ，－λ)，所以PA�＝1PD�―→＋1DA�＝(－λ，－λ，λ)＋(1,0，－1)＝(1－λ，－λ，λ－1)，PC�＝1PD�＋1DC�＝(－λ，－λ，λ)＋(0,1，－1)＝(－λ，1－λ，λ－1)．显然∠APC不是平角，所以∠APC为钝角等价于cos∠APC＝cos〈PA�，PC�〉＝PAPCPAPC��<0，这等价于PA�·PC�<0，即(1－λ)(－λ)＋(－λ)(1－λ)＋(λ－1)2＝(λ－1)(3λ－1)<0，得<λ<1.因此，λ的取值范围为.7．如图，P－ABCD是正四棱锥，ABCD－A1B1C1D1是正方体，其中AB＝2，PA＝.(1)求证：PA⊥B1D1；(2)求平面PAD与平面BDD1B1所成锐二面角的余弦值．解：以D1为原点，D1A1所在直线为x轴，D1C1所在直线为y轴，D1D所在直线为z轴建立空间直角坐标系，则D1(0,0,0)，A1(2,0,0)，B1(2,2,0)，C1(0,2,0)，D(0,0,2)，A(2,0,2)，B(2,2,2)，C(0,2,2)，P(1,1,4)．(1)证明： AP�＝(－1,1,2)，11DB�＝(2,2,0)，∴AP�·11DB�＝－2＋2＋0＝0，∴PA⊥B1D1.(2)平面BDD1B1的法向量为AC�＝(－2,2,0)．DA�＝(2,0,0)，3OP�＝(1,1,2)．设平面PAD的法向量为n＝(x，y，z)，则n⊥DA�，n⊥DP�.∴∴取n＝(0，－2,1)，设所求锐二面角为θ，则cosθ＝nACnAC��＝＝.8．(2010·广州调研)如图，已知等腰直角三角形RBC，其中∠RBC＝90°，RB＝BC＝2.点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连结PB、PC.(1)求证：BC⊥PB；(2)求二面角A－CD－P的平面角的余弦值．解：(1)...