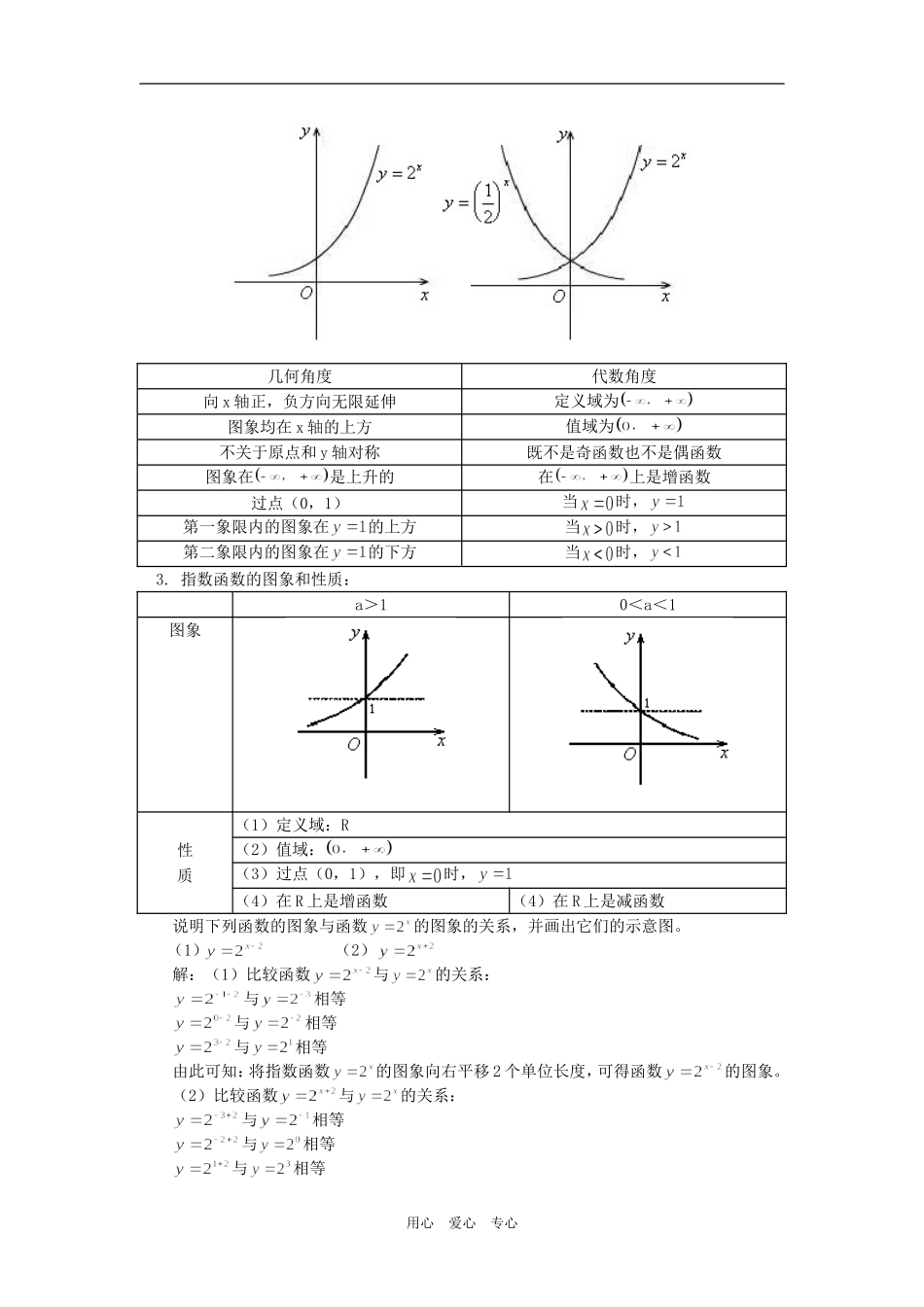
高一数学指数函数苏教版【本讲教育信息】一.教学内容:指数函数【教学目标】1.了解指数函数模型的实际背景,认识学习指数函数的必要性;理解分数指数幂的含义,了解实数指数幂的意义,理解n次方根与n次根式的概念,熟练掌握用根式与分数指数幂表示一个正数的算术根;能运用有理指数幂的运算性质进行运算和化简,会进行根式与分数指数幂的相互转化。2.理解指数函数的含义及性质,能利用函数图象的平移与对称变换,讨论指数函数的图象;能运用指数函数的单调性,比较两个指数数值的大小,会求一类与指数函数有关的复合函数的定义域、值域、单调性等。了解函数图象的平移变换。【教学过程】一.分数指数幂:(一)根式如果一个数的平方等于a,那么这个数叫做a的平方根;如果一个数的立方等于a,那么这个数叫做a的立方根。例如:若32=9,则3是9的平方根;若53=125,则5是125的立方根;若24=16,则2是16的4次方根;若35=243,则3是243的5次方根。1.n次方根的定义:一般地,如果一个数的n(n>1,n∈N*)次方等于a,那么这个数叫做a的n次方根。即若,则x叫做a的n次方根,其中n>1,且n∈N*。当n是奇数时,实数a的n次方根用符号表示;当n是偶数时,正数a的n次方根用符号表示。式子叫做根式,其中n叫做根指数,a叫做被开方数。例如:27的3次方根表示为的5次方根表示为的3次方根表示为16的4次方根表示为±,即16的4次方根有两个,一个是,另一个是,它们绝对值相等而符号相反。2.方根的性质:奇次方根的性质:在实数范围内,正数的奇次方根是一个正数;负数的奇次方根是一个用心爱心专心负数。例如:。偶次方根的性质:在实数范围内,正数的偶次方根是两个绝对值相等符号相反的数;负数的偶次方根没有意义。例如:16的4次方根是;而的4次方根则没有意义。0的任何次方根都是0,记作。3.二组常用公式:(1)当n为任意正整数时,。(2)(二)分数指数幂1.(1)正数的正分数指数幂的定义:(2)负分数指数幂的意义:我们规定:0的正分数指数幂等于0;0的负分数指数幂没有意义。2.有理数指数幂的运算性质(1)(2)(3)二.指数函数:现在大家来看下面的问题:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系式是。1.指数函数定义:一般地,函数叫做指数函数,其中x是自变量,函数定义域是R。2.与的图象:用心爱心专心几何角度代数角度向x轴正,负方向无限延伸定义域为图象均在x轴的上方值域为不关于原点和y轴对称既不是奇函数也不是偶函数图象在是上升的在上是增函数过点(0,1)当时,第一象限内的图象在的上方当时,第二象限内的图象在的下方当时,3.指数函数的图象和性质:a>10<a<1图象(1)定义域:R性(2)值域:质(3)过点(0,1),即时,(4)在R上是增函数(4)在R上是减函数说明下列函数的图象与函数的图象的关系,并画出它们的示意图。(1)(2)解:(1)比较函数与的关系:与相等与相等与相等由此可知:将指数函数的图象向右平移2个单位长度,可得函数的图象。(2)比较函数与的关系:与相等与相等与相等用心爱心专心由此可知:将指数函数的图象向左平移2个单位长度,可得函数的图象。思考:指出的图象与及的图象之间的关系。结论:一般地,函数图象平移交换时,h>0时,将的图象向右平移h个单位后得到的图象;向左平移h个单位后,得到的图象;将的图象向上平移h个单位后,得到的图象;将的图象向下平移h个单位后,得到的图象。【典型例题】例1.求值:(1);(2);(3);(4);(5)解:(1)(2)(3)(4)(5)例2.计算:(1)(2)用心爱心专心答:(1)原式(2)原式=1例3.比较大小:(1)(2)(3)解:(1)考虑指数函数在R上的增函数又2.5<3.2,(2)小于(3)大于例4.解下列不等式:(1);(2)解:(1)原式可化为:,因为为增函数,即(2)可化为:即例5.(1)求函数的定义域、值域及单调递增区间。解:定义域为R而是R上减函数用心爱心专心令则y在R上为减函数当时当时所以当时,y是减函数当时,y是增函数(2)下列函数中,值域是的是()A.B.C.D.答案:C解:A中,,所以值域不是B中,,所以值域不...