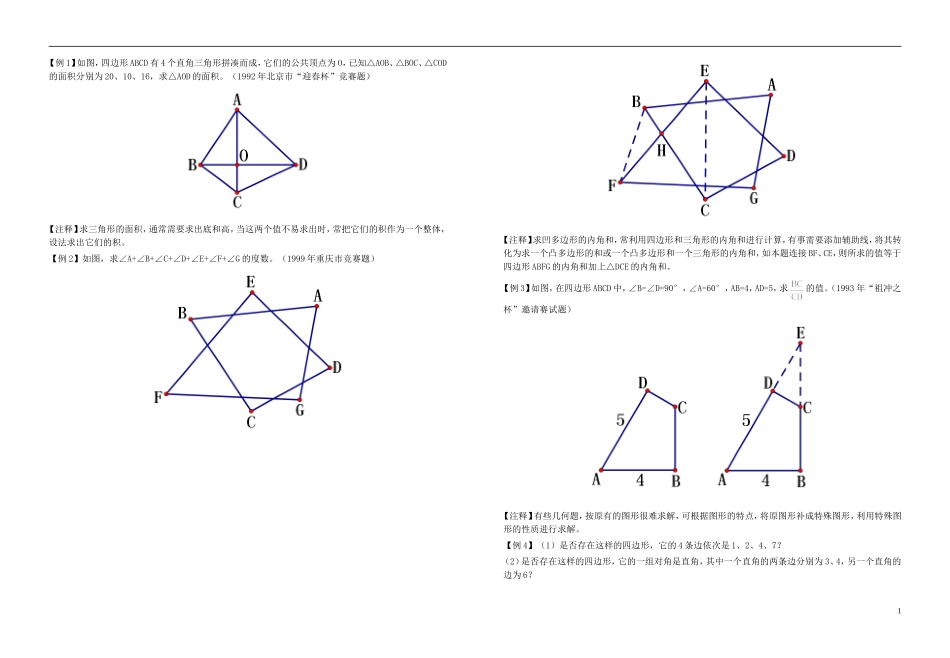
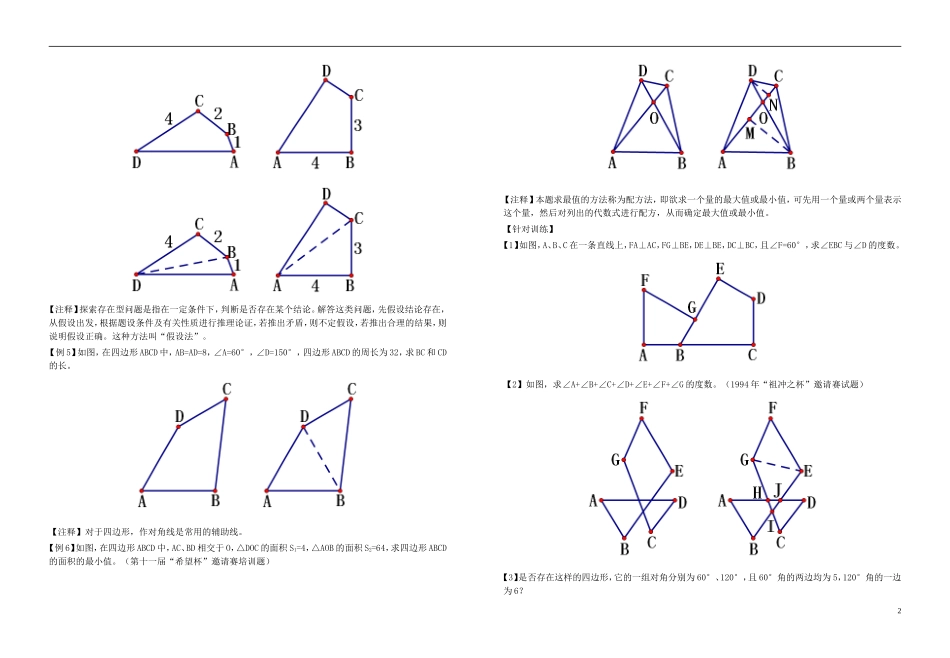
【例1】如图,四边形ABCD有4个直角三角形拼凑而成,它们的公共顶点为O,已知△AOB、△BOC、△COD的面积分别为20、10、16,求△AOD的面积。(1992年北京市“迎春杯”竞赛题)【注释】求三角形的面积,通常需要求出底和高,当这两个值不易求出时,常把它们的积作为一个整体,设法求出它们的积。【例2】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。(1999年重庆市竞赛题)【注释】求凹多边形的内角和,常利用四边形和三角形的内角和进行计算,有事需要添加辅助线,将其转化为求一个凸多边形的和或一个凸多边形和一个三角形的内角和,如本题连接BF、CE,则所求的值等于四边形ABFG的内角和加上△DCE的内角和。【例3】如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,AD=5,求的值。(1993年“祖冲之杯”邀请赛试题)【注释】有些几何题,按原有的图形很难求解,可根据图形的特点,将原图形补成特殊图形,利用特殊图形的性质进行求解。【例4】(1)是否存在这样的四边形,它的4条边依次是1、2、4、7?(2)是否存在这样的四边形,它的一组对角是直角,其中一个直角的两条边分别为3、4,另一个直角的边为6?1【注释】探索存在型问题是指在一定条件下,判断是否存在某个结论。解答这类问题,先假设结论存在,从假设出发,根据题设条件及有关性质进行推理论证,若推出矛盾,则不定假设,若推出合理的结果,则说明假设正确。这种方法叫“假设法”。【例5】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32,求BC和CD的长。【注释】对于四边形,作对角线是常用的辅助线。【例6】如图,在四边形ABCD中,AC、BD相交于O,△DOC的面积S1=4,△AOB的面积S2=64,求四边形ABCD的面积的最小值。(第十一届“希望杯”邀请赛培训题)【注释】本题求最值的方法称为配方法,即欲求一个量的最大值或最小值,可先用一个量或两个量表示这个量,然后对列出的代数式进行配方,从而确定最大值或最小值。【针对训练】【1】如图,A、B、C在一条直线上,FA⊥AC,FG⊥BE,DE⊥BE,DC⊥BC,且∠F=60°,求∠EBC与∠D的度数。【2】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。(1994年“祖冲之杯”邀请赛试题)【3】是否存在这样的四边形,它的一组对角分别为60°、120°,且60°角的两边均为5,120°角的一边为6?2【4】如图,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB于E。若四边形ABCD的面积为8,求DE的长。(1996年四川省竞赛题)【5】在四边形ABCD中,AB=2,BC=4,CD=7,求AD的取值范围。【6】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠ADC=135°,AE=(AD+AB),BC=2。求BE的长。【例1】已知:四边形ABCD,从(1)AB∥DC;(2)AB=DC;(3)AD∥BC;(4)AD=BC;(5)∠A=∠C;(6)∠B=∠D中取出两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请具体写出这些组合。(1998年江苏省竞赛题)【注释】解四边形问题,常需要判定其形状,要熟记判定定理;由于判定定理比较多,易混易忘,可从边、角、对角线3个方面加以记忆。【例2】凸四边形ABCD中,AB∥CD,且AB+BC=CD+AD。求证:ABCD是平行四边形。(1990年芜湖市竞赛题)3【例3】平面上有三个正△ABD、△ACE、△BCF,两两共有一个顶点。求证:CD与EF互相平分。(1990年芜湖市竞赛题)【例4】在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE。求证:FK∥AB。(大连市第八届“育英杯”竞赛题)【注释】对于求证线段相等,角相等,线段互相平行,两线平行,两线垂直等问题,常先判定出某个四边形是平行四边形或特殊的平行四边形,再根据其性质进行证明。这种证明方法往往优于用三角形的性质证明的方法。【例5】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。证明:不论E、F怎样移动,△BEF总是正三角形。(1990年合肥市竞赛题)【注释】对于平行四边形问题,常将其转化为三角形问题解决。解题时要注意利用平行四边形的性质,这些性质往往为解题提供必要的条件。【例6】矩形ABCD中,AB=20cm,BC=10cm。...