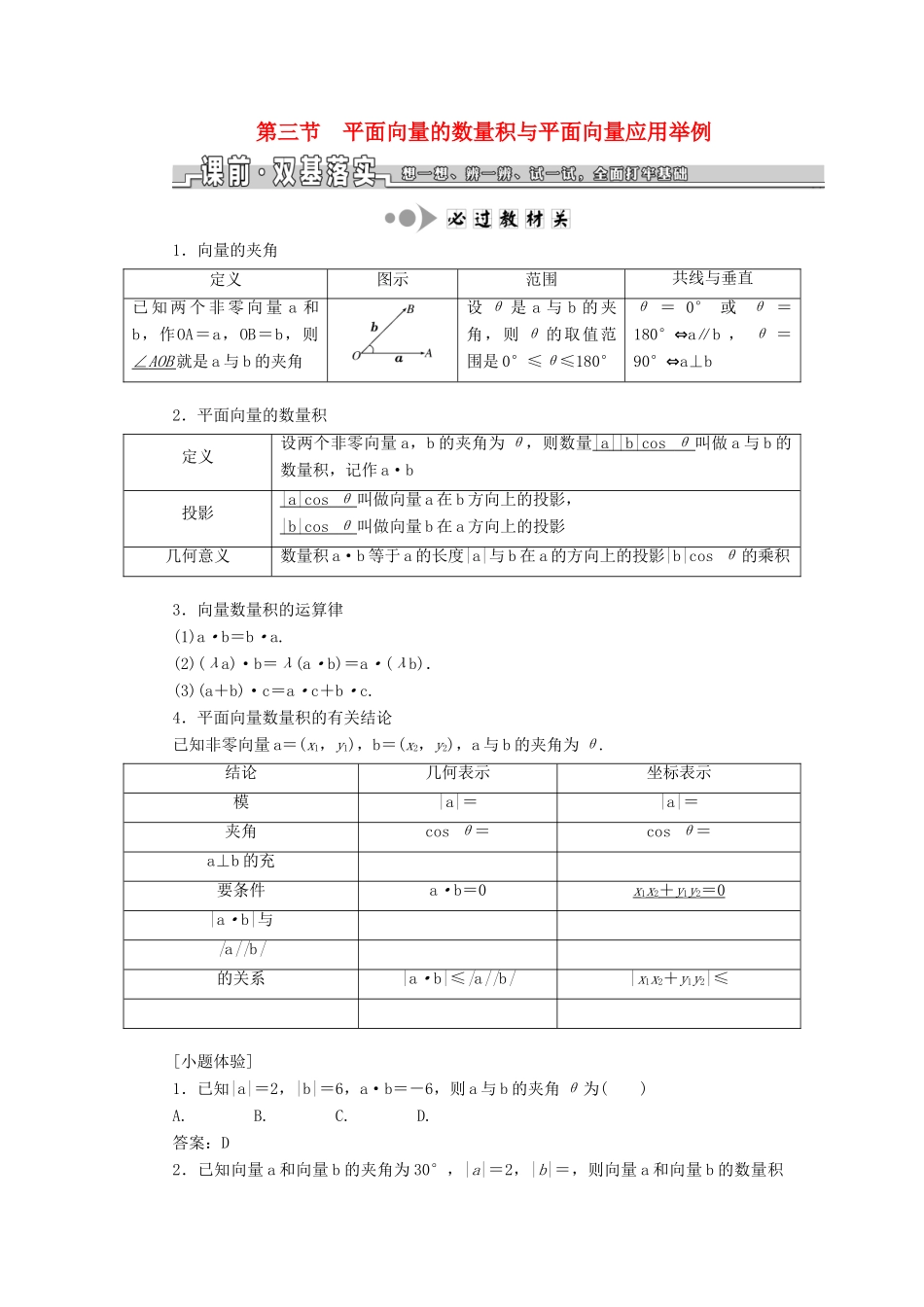
第三节平面向量的数量积与平面向量应用举例1.向量的夹角定义图示范围共线与垂直已知两个非零向量a和b,作OA=a,OB=b,则∠AOB就是a与b的夹角设θ是a与b的夹角,则θ的取值范围是0°≤θ≤180°θ=0°或θ=180°⇔a∥b,θ=90°⇔a⊥b2.平面向量的数量积定义设两个非零向量a,b的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b投影|a|cosθ叫做向量a在b方向上的投影,|b|cosθ叫做向量b在a方向上的投影几何意义数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积3.向量数量积的运算律(1)a·b=b·a.(2)(λa)·b=λ(a·b)=a·(λb).(3)(a+b)·c=a·c+b·c.4.平面向量数量积的有关结论已知非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ.结论几何表示坐标表示模|a|=|a|=夹角cosθ=cosθ=a⊥b的充要条件a·b=0x1x2+y1y2=0|a·b|与|a||b|的关系|a·b|≤|a||b||x1x2+y1y2|≤[小题体验]1.已知|a|=2,|b|=6,a·b=-6,则a与b的夹角θ为()A.B.C.D.答案:D2.已知向量a和向量b的夹角为30°,|a|=2,|b|=,则向量a和向量b的数量积a·b=()A.1B.2C.3D.4解析:选C由题意可得a·b=|a|·|b|·cos〈a,b〉=2××=3.3.已知向量a,b均为单位向量,若它们的夹角为60°,则|a+3b|=()A.B.C.D.4解析:选C依题意得a·b=,则|a+3b|==.4.已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b.若b·c=0,则t=________.解析:因为向量a,b为单位向量,所以b2=1,又向量a,b的夹角为60°,所以a·b=,由b·c=0,得b·[ta+(1-t)b]=0,即ta·b+(1-t)b2=0,所以t+(1-t)=0,所以t=2.答案:25.已知正方形ABCD的边长为2,E为CD的中点,则AE·BD=________.解析:选向量的基底为AB,AD,则BD=AD-AB,AE=AD+AB,所以AE·BD=·(AD-AB)=2.答案:21.数量积运算律要准确理解、应用,例如,a·b=a·c(a≠0)不能得出b=c,两边不能约去一个向量.2.两个向量的夹角为锐角,则有a·b>0,反之不成立;两个向量夹角为钝角,则有a·b<0,反之不成立.3.a·b=0不能推出a=0或b=0,因为a·b=0时,有可能a⊥b.4.在用|a|=求向量的模时,一定要把求出的a2再进行开方.[小题纠偏]1.若a,b是两个互相垂直的非零向量,给出以下式子:①a·b=0;②a+b=a-b;③|a+b|=|a-b|;④a2+b2=(a+b)2.其中正确的个数是()A.1B.2C.3D.4解析:选C因为a,b是两个互相垂直的非零向量,所以a·b=0;所以(a+b)2=a2+b2+2a·b=a2+b2;(a-b)2=a2+b2-2a·b=a2+b2;所以(a+b)2=(a-b)2,即|a+b|=|a-b|.故①③④是正确的,②是错误的.2.设向量a,b满足|a|=|b|=1,a·b=-,则|a+2b|=________.解析:|a+2b|====.答案:[题组练透]1.设a=(1,-2),b=(-3,4),c=(3,2),则(a+2b)·c=()A.(-15,12)B.0C.-3D.-11解析:选C a+2b=(1,-2)+2(-3,4)=(-5,6),∴(a+2b)·c=(-5,6)·(3,2)=-3.2.(2018·浙江考前冲刺)若两个非零向量a,b满足|a+b|=|a-b|=2|b|=4,则向量a在a+b上的投影为()A.B.3C.D.6解析:选B由|a+b|=|a-b|,得a2+2a·b+b2=a2-2a·b+b2,即a·b=0,由|a+b|=2|b|,得a2+2a·b+b2=4b2,即a2=3b2,所以|a|=|b|=2,所以向量a在a+b上的投影为==3.3.如图,在等腰直角三角形ABC中,∠C=90°,AC=2,D为BC的中点,则AB·AD=________.解析:法一:由题意知,AC=BC=2,AB=2,∴AB·AD=AB·(AC+CD)=AB·AC+AB·CD=|AB|·|AC|cos45°+|AB|·|CD|cos45°=2×2×+2×1×=6.法二:建立如图所示的平面直角坐标系,由题意得A(0,2),B(-2,0),D(-1,0),∴AB=(-2,0)-(0,2)=(-2,-2),AD=(-1,0)-(0,2)=(-1,-2),∴AB·AD=-2×(-1)+(-2)×(-2)=6.答案:64.(2019·台州模拟)以O为起点作三个不共线的非零向量OA,OB,OC,使AB=-2BC,|OA|=4,+=,则OA·BC=________.解析:法一:由+=,平方得·=-,即cos∠AOB=-,因为OA,OB不共线,所以0°<∠AOB<180°,所以∠AOB=120°.因为AB=-2BC,所以C为线段AB的中点.由+=...