《指数函数》教案（1）VIP免费

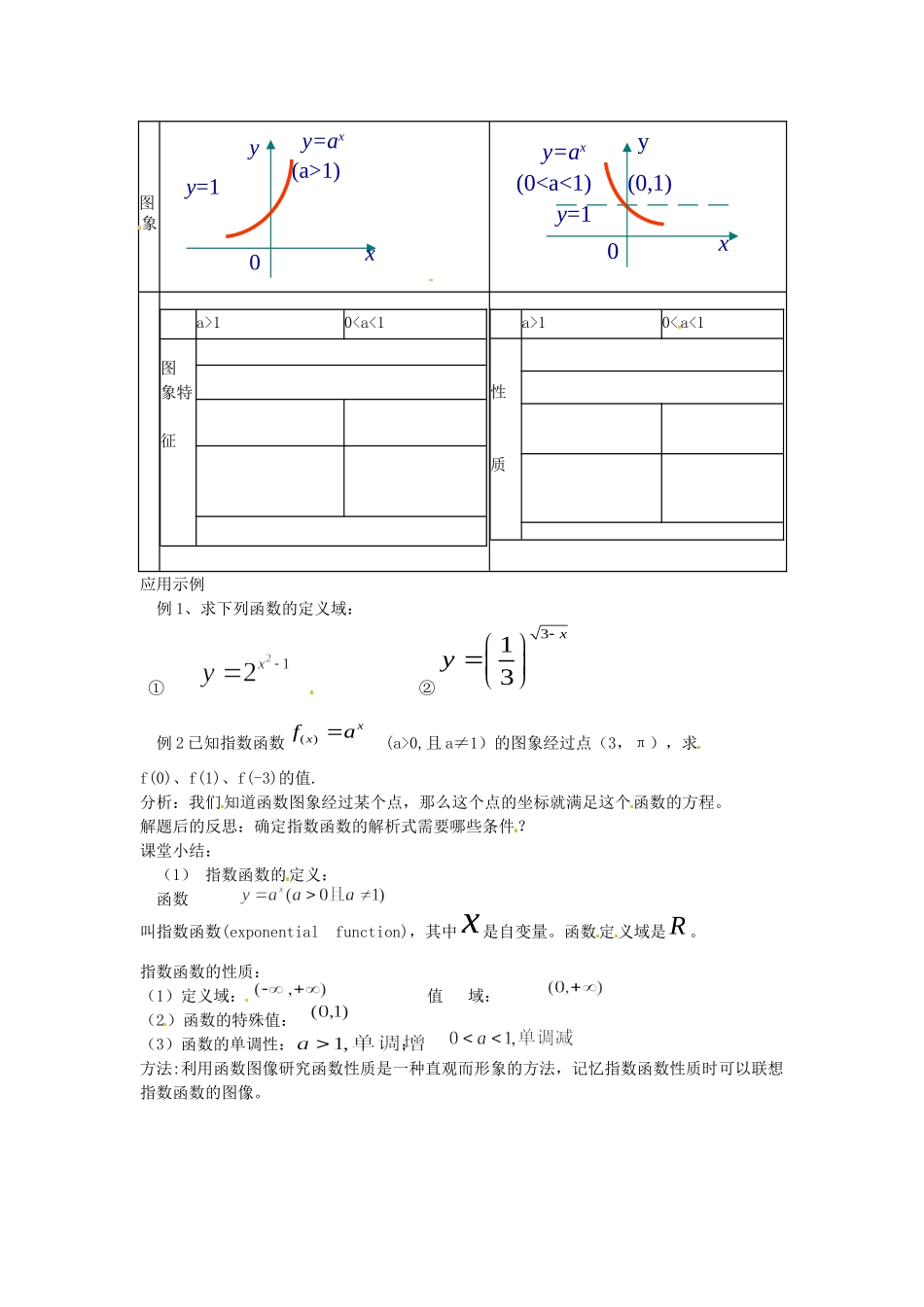
指数函数及其性质教学目标：知识技能：使学生理解指数函数的定义，掌握指数函数的图象和性质，初步学会运用指数函数解决问题。过程方法：引入，剖析、定义指数函数的过程，启动观察、分析、归纳、总结、抽象概括等思维活动，培养学生的思维能力，体会数学概念的学习方法，通过运用多媒体的教学手段，引领学生主动探索指数函数性质，体会学习数学规律的方法，体验成功的乐趣.情感态度和价值观：通过本节课的学习，使学生获得研究函数的规律和方法，提高学生的学习能力，养成积极主动，勇于探索，不断创新的学习习惯和品质。教学重难点重点：指数函数的定义、图象、性质.难点：指数函数的定义理解，指数函数的图象特征及指数函数的性质。教学媒体：多媒体教室教学过程：创设问题情境引例1：某种细胞分裂时，由1个分裂成2个，2个分裂成4个，......,依此类推，一个这样的细胞分裂x次后，得到的细胞个数y与分裂次数x有怎样的函数关系？引例2：某种商品的价格从今年起每年降低15%，设原来的价格为1，x年后的价格为y，则y与x的函数关系式？引导学生分析问题通过列表寻找规律动画展示细胞分裂的过程，寻找Y于X的对应关系，进而得到得到的细胞个数y与分裂次数x的函数关系。通过列表：寻找商品价格y与x年后的函数关系。归纳总结：函数关系：12xy20.85xy在12xy和20.85xy中，指数x是自变量，底数是一个大于0且不等于1的常量。我们把这种自变量在指数位置，而底数是大于0不等于1的常量的函数称为指数函数。新知探究指数函数的定义：函数叫指数函数(exponentialfunction)，其中x是自变量。函数定义域是R。探究1：为什么要规定0,1aa且呢？x1234562y0.8520.8530.8540.8550.8560.85练习1：若是指数函数，求a的取值范围。探究2：函数23xy是指数函数吗？练习2：下列函数是否是指数函数：（1）y=0.2x(2)y=(-2)x(3)y=ex(4)3xy(5)y=1x本题主要考察学生对指数函数定义的理解。特别注意底数10aa且。问题：在前面，我们是如何来研究函数的性质的呢？问题：研究函数的性质，考虑哪些方面？今天，我们借鉴研究函数性质的方法通过借助函数的图像来研究指数函数的性质。观察下面指数函数的图像，你能发现它们的函数图像有哪些特征？将2xy，3xy和12xy，13xy的图像画在同一个直角坐标。问题一：图象分别在哪几个象限？问题二：图象的上升、下降与底数a有联系吗？问题三：图象中有哪些特殊的点？问题四：指数函数2xy的图像是否具有对称性？问题五：函数3xy与13xy图象有什么关系？猜想：函数xay与xay)1(关于Y轴对称。分析：函数xay图像上的点(,)xxa关于Y轴对称的点(,)xxa，该点坐标还可可表示为1(,())xxa在xay)1(的图像上；xay)1(图像上的点1(,())xxa关于Y轴对称的点1(,())xxa，该点坐标还可可表示为(,)xxa在xay图像上。因此，猜想是正确的。用几何画板演示当底数0,1aa且时的指数函数图象。完成下表：图像和性质a>1010100,且a≠1）的图象经过点（3，π），求f(0)、f(1)、f(-3)的值.分析：我们知道函数图象经过某个点，那么这个点的坐标就满足这个函数的方程。解题后的反思：确定指数函数的解析式需要哪些条件？课堂小结：（1）指数函数的定义：函数叫指数函数(exponentialfunction)，其中x是自变量。函数定义域是R。指数函数的性质：（1）定义域：值域：（2）函数的特殊值：（3）函数的单调性：；方法:利用函数图像研究函数性质是一种直观而形象的方法，记忆指数函数性质时可以联想指数函数的图像。xy0y=1y=ax(a>1)y0(0