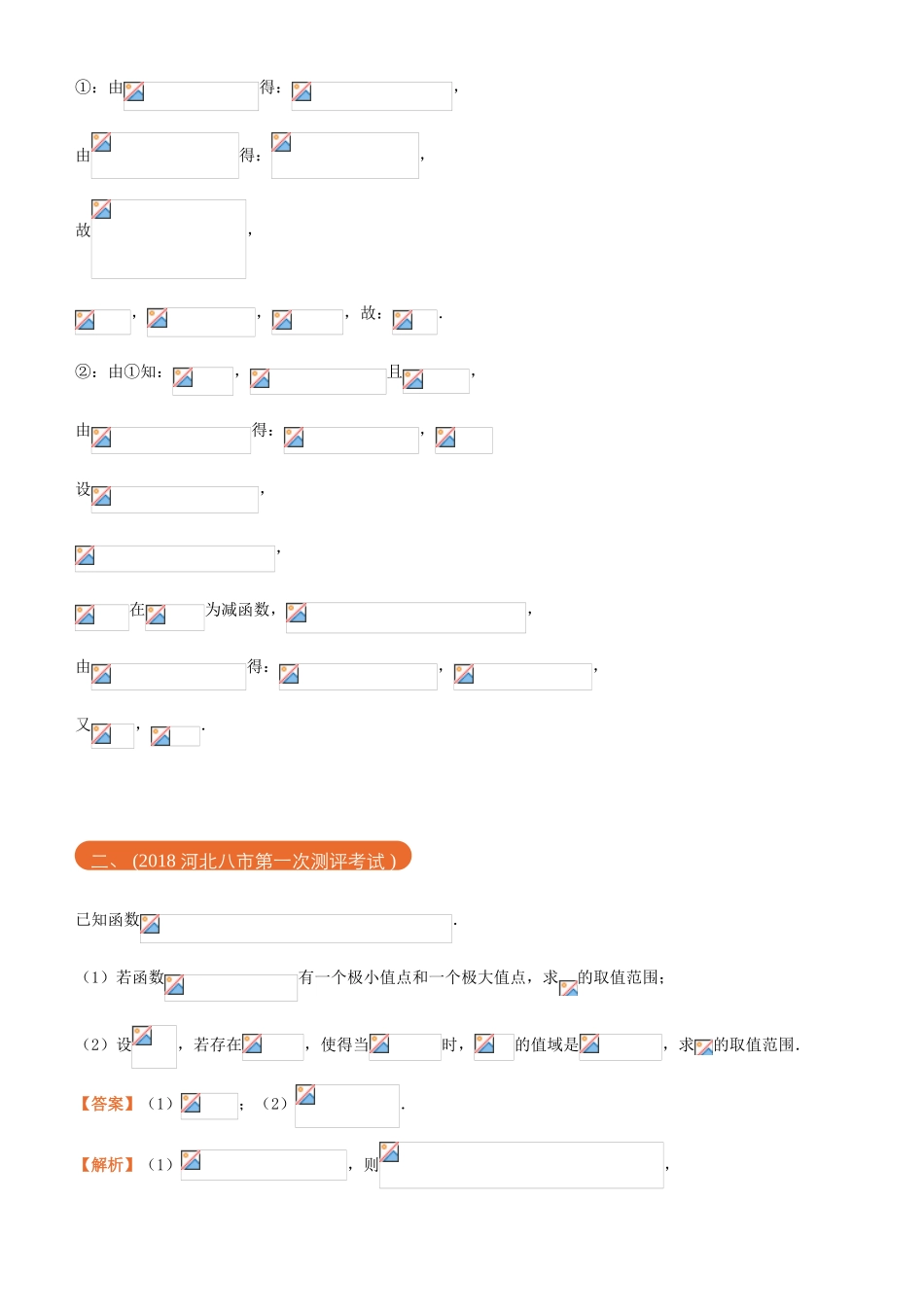
函数、导数之一存在与恒成立问题已知函数,,.(1)当时,若对任意均有成立,求实数的取值范围;(2)设直线与曲线和曲线相切,切点分别为,,其中.①求证:;②当时,关于的不等式恒成立,求实数的取值范围.【答案】(1);(2)①证明见解析;②.【解析】(1)当时,,由知:,依题意:对恒成立,设,,当时;当时,,设,,当时;当时,,故实数的取值范围是.(2)由已知:,,一、(2018东北三省三校(哈师大附中、东北师大附中、辽宁实验中学)一模)①:由得:,由得:,故,,,,故:.②:由①知:,且,由得:,设,,在为减函数,,由得:,,又,.已知函数.(1)若函数有一个极小值点和一个极大值点,求的取值范围;(2)设,若存在,使得当时,的值域是,求的取值范围.【答案】(1);(2).【解析】(1),则,二、(2018河北八市第一次测评考试)令,若函数有两个极值点,则方程必有两个不等的正根,设为,,不妨设,于是,解得,则.当时,,,在上为减函数;当时,,,在上为增函数;当时,,函数在上为减函数.由此,是函数的极小值点,是函数的极大值点.符合题意.综上,所求实数的取值范围是.(2),①当时,.当时,,在上为减函数;当时,,在上为增函数.所以,当时,,的值域是.不符合题意.②当时,.(i)当,即时,,当且仅当时取等号.所以在上为减函数.从而在上为减函数.符合题意.(ii)当,即时,当变化时,,的变化情况如下表:减函数极小值增函数极大值减函数若满足题意,只需满足,且(若,不符合题意),即,且.又,所以,此时.所以实数的取值范围是.已知函数.(1)设,讨论的单调性;(2)若不等式恒成立,其中为自然对数的底数,求的最小值.【答案】(1)见解析;(2).【解析】(1)函数定义域为,由题意得,则,①当时,,则在上单调递增;②当时,令,解得,三、(2018百校联盟TOP20高三三月联考)当时,,在上单调递增,当时,,在上单调递减.(2)设函数,其中为自然对数的底数,∴,,当时,,在上是增函数,∴不可能恒成立,当时,由,得,∵不等式恒成立,∴,当时,,单调递增,当时,,单调递减,∴当时,取最大值,,∴满足即可,∴,∴,令,,.令,,由,得,当时,,是增函数,当时,,是减函数,∴当时,取最小值,∵且当时,,∴当时,;当时,.∴当时,,是减函数,当时,,是增函数,∴时,取最小值,,∴的最小值为.