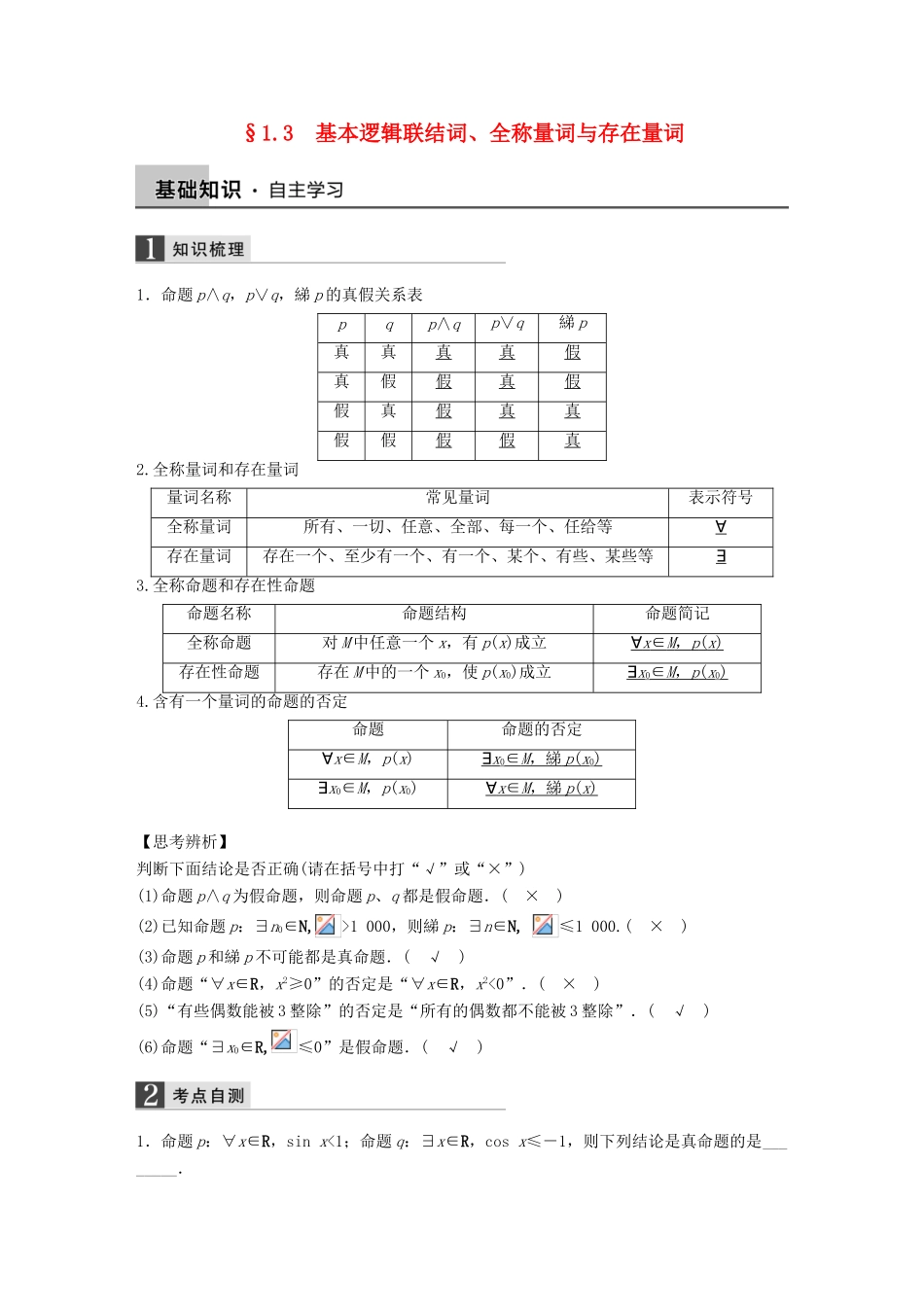
§1.3基本逻辑联结词、全称量词与存在量词1.命题p∧q,p∨q,綈p的真假关系表pqp∧qp∨q綈p真真真真假真假假真假假真假真真假假假假真2.全称量词和存在量词量词名称常见量词表示符号全称量词所有、一切、任意、全部、每一个、任给等∀存在量词存在一个、至少有一个、有一个、某个、有些、某些等∃3.全称命题和存在性命题命题名称命题结构命题简记全称命题对M中任意一个x,有p(x)成立∀x∈M,p(x)存在性命题存在M中的一个x0,使p(x0)成立∃x0∈M,p(x0)4.含有一个量词的命题的否定命题命题的否定∀x∈M,p(x)∃x0∈M,綈p(x0)∃x0∈M,p(x0)∀x∈M,綈p(x)【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)命题p∧q为假命题,则命题p、q都是假命题.(×)(2)已知命题p:∃n0∈N,>1000,则綈p:∃n∈N,≤1000.(×)(3)命题p和綈p不可能都是真命题.(√)(4)命题“∀x∈R,x2≥0”的否定是“∀x∈R,x2<0”.(×)(5)“有些偶数能被3整除”的否定是“所有的偶数都不能被3整除”.(√)(6)命题“∃x0∈R,≤0”是假命题.(√)1.命题p:∀x∈R,sinx<1;命题q:∃x∈R,cosx≤-1,则下列结论是真命题的是________.①p∧q;②綈p∧q;③p∨綈q;④綈p∧綈q.答案②解析 p是假命题,q是真命题,∴綈p∧q是真命题.2.(2013·重庆改编)命题“对任意x∈R,都有x2≥0”的否定为________.答案存在x0∈R,使得x<0解析因为“∀x∈M,p(x)”的否定是“∃x0∈M,綈p(x0)”,故“对任意x∈R,都有x2≥0”的否定是“存在x0∈R,使得x<0”.3.(2014·重庆改编)已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件.则下列命题为真命题的是________.①p∧q;②綈p∧綈q;③綈p∧q;④p∧綈q.答案④解析因为指数函数的值域为(0,+∞),所以对任意x∈R,y=2x>0恒成立,故p为真命题;因为当x>1时,x>2不一定成立,反之当x>2时,一定有x>1成立,故“x>1”是“x>2”的必要不充分条件,故q为假命题,则p∧q、綈p为假命题,綈q为真命题,綈p∧綈q、綈p∧q为假命题,p∧綈q为真命题,故④正确.4.若命题“∃x∈R,x2-mx-m<0”是假命题,则实数m的取值范围是________.答案[-4,0]解析“∃x∈R,x2-mx-m<0”是假命题,则“∀x∈R,x2-mx-m≥0”是真命题.即Δ=m2+4m≤0,∴-4≤m≤0.题型一含有逻辑联结词命题的真假判断例1(1)命题p:将函数y=sin2x的图象向右平移个单位得到函数y=sin的图象;命题q:函数y=sincos的最小正周期为π,则命题“p∨q”“p∧q”“綈p”中真命题的个数是________.(2)已知命题p:若a>1,则ax>logax恒成立;命题q:在等差数列{an}中,m+n=p+q是an+am=ap+aq的充分不必要条件(m,n,p,q∈N*).则下面选项中真命题是________.①(綈p)∧(綈q)②(綈p)∨(綈q)③p∨(綈q)④p∧q答案(1)2(2)②解析(1)函数y=sin2x的图象向右平移个单位后,所得函数为y=sin=sin,∴命题p是假命题.又y=sincos=sincos=sin2=-cos,∴其最小正周期为T==π,∴命题q真.由此,可判断命题“p∨q”真,“p∧q”假,“綈p”为真.所以真命题的个数是2.(2)当a=1.1,x=2时,ax=1.12=1.21,logax=log1.12>log1.11.21=2,此时,axy,则-x<-y;命题q:若x>y,则x2>y2.在命题①p∧q;②p∨q;③p∧(綈q);④(綈p)∨q中,真命题是________.(2)“p或q”为真命题是“p且q”为真命题的________条件.答案(1)②③(2)必要不充分解析(1)当x>y时,-x<-y,故命题p为真命题,从而綈p为假命题.当x>y时,x2>y2不一定成立,故命题q为假命题,从而綈q为真命题.由真值表知,①p∧q为...