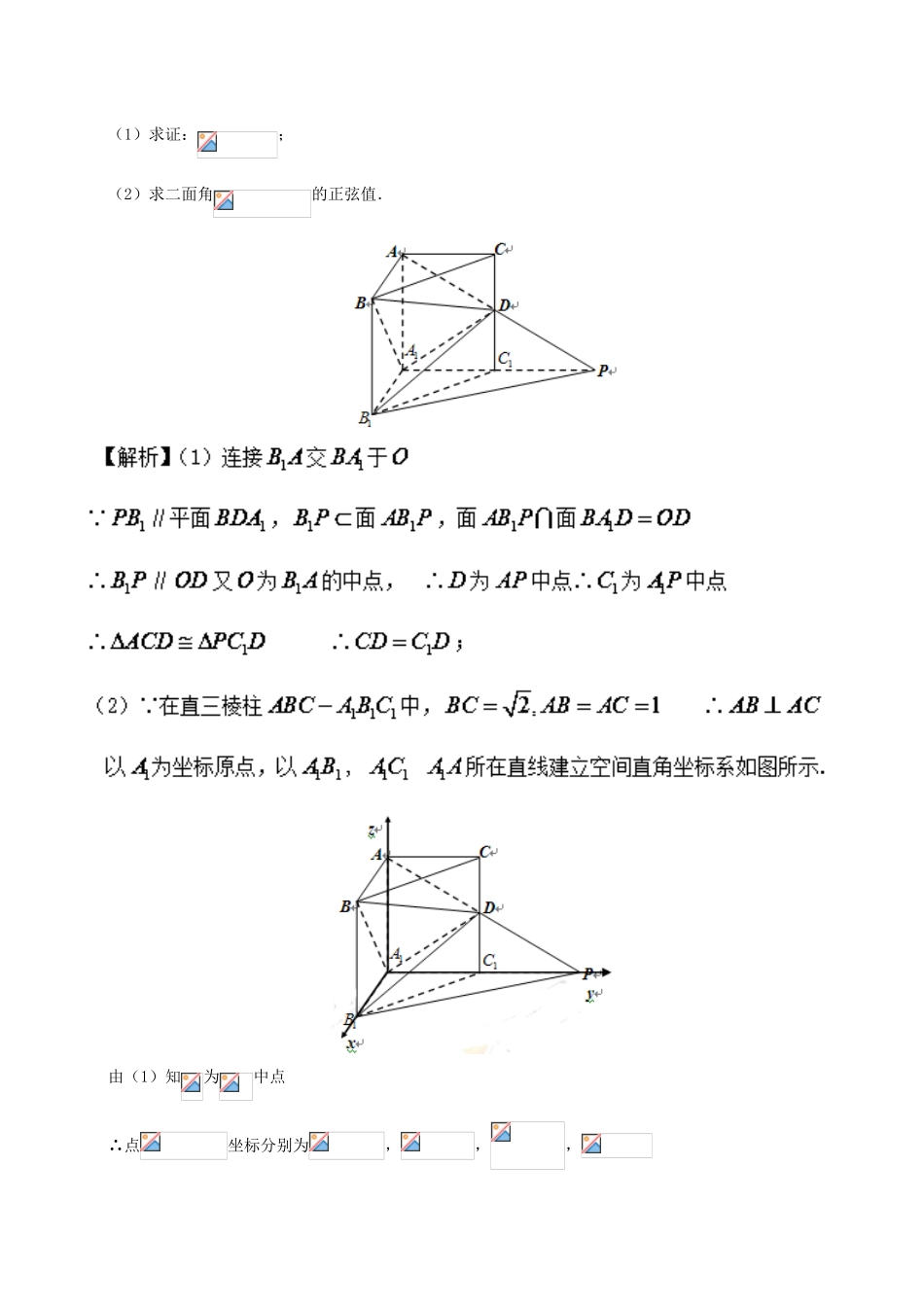
第51讲空间几何点的坐标的写法【知识要点】一、空间向量的正交分解空间的任意向量,均可分解为不共面的三个向量、、,使.如果两两垂直,这种分解就是空间向量的正交分解.二、空间向量基本定理如果三个向量不共面,那么对于空间任意一个向量,存在一个唯一的有序实数组使.我们把叫做空间的一个基底,其中叫基向量.三、单位正交分解如果空间一个基底的三个基向量互相垂直,长度都为1个单位,则这个基底叫做单位正交基底,通常用{}表示.四、空间直角坐标若为有公共起点的三个两两垂直的单位向量,分别以的方向为轴,轴,轴的正方向建立空间直角坐标系,有序实数组使得,我们把称作向量在单位正交基底下的坐标,记作,则坐标就是向量的坐标.五、写空间点的坐标常用的有直接观察法、向量法、作坐标线法三种.【方法讲评】方法一直接观察法使用情景点的位置比较特殊,一般在坐标轴上或其它特殊位置.解题步骤直接利用空间向量点坐标的定义观察写出点的坐标.【例1】如图,在直三棱柱中,,是棱上的一点,是的延长线与的延长线的交点,且∥平面.(1)求证:;(2)求二面角的正弦值.由(1)知为中点∴点坐标分别为,,,设平面的法向量 且∴取【点评】该题中的几何体比较特殊的几何体直三棱柱,题目中的各个点比较容易直接观察得到,所以选择直接观察法写出各点的坐标.在正方体、长方体、直棱柱、正棱柱等特殊几何体中也常用直接观察法.【反馈检测1】如图,在四棱锥中,底面是正方形,侧棱⊥底面,,是的中点,作交于点.(1)求证:平面;(2)求二面角的正弦值.方法二向量法使用情景点在一般位置,不是特殊位置.解题步骤利用向量的关系计算出空间点的坐标.【例2】己知四棱锥,其中底面为矩形侧棱,其中,,为侧棱上的两个三等分点,如图所示:(1)求证:;(2)求二面角的余弦值.(2)易知为等腰直角三角形,所以为外接圆的直径,所以,,如图所示,以为原点,建立空间直角坐标系,则(0,0,0),(3,0,0),(3,6,0),(0,6,0),(0,0,3),设坐标为,由题得,所以所以,所以坐标为(2,4,1),同理点坐标为(1,2,2),设平面的法向量为,,并且,,令得,【点评】本题中的点的坐标不是很好写,所以要根据向量的关系列出方程,再解方程即可推算出的坐标.【例3】如图,在各棱长均为2的三棱柱中,侧面,.(Ⅰ)求侧棱与平面所成角的正弦值的大小;(Ⅱ)已知点满足,在直线上是否存在点,使∥平面?若存在,请确定点的位置;若不存在,请说明理由.【解析】(Ⅰ) 侧面,作于点,∴.又,且各棱长都相等,∴,,故以为坐标原点,建立如图所示的空间直角坐标系,则(0,﹣1,0),(,0,0),,(0,1,0),.(Ⅱ) ,而∴.又 ,∴点的坐标为.假设存在点符合题意,则点的坐标可设为.∴ ∥平面,为平面的法向量,∴由,得,∴.又,故存在点,使∥平面,其坐标为,即恰好为点.【点评】本题中的点的坐标不是很好写,但是利用列出关于点坐标的方程便可以比较方便地写出它的坐标.【反馈检测2】正三棱锥的三条侧棱两两垂直,且长度均为2.分别是的中点,是的中点,过的一个平面与侧棱或其延长线分别相交于,已知.(1)证明:平面;(2)求二面角的余弦值;(3)求点到平面的距离.方法三作坐标线法使用情景点所在的三角形是直角三角形.解题步骤作出点的坐标线,根据坐标线写出点的坐标.【例4】如图,四棱锥的底面为矩形,且,,,.(Ⅰ)求证:;(Ⅱ)求直线与平面所成角的正弦值.(Ⅱ)以点为坐标原点,所在的直线为轴建立空间直角坐标系如右图示,则依题意可得,可得平面的单位法向量为,设直线与平面所成角为,则∴,即直线与平面所成角的正弦值为.【点评】本题中点的坐标,直接观察不是很方便,需要过点作,垂足为,再解三角形,得到的长度,即可得到点的坐标.【反馈检测3】如图在底面为菱形的四棱锥,,点在上,且.(Ⅰ)求证:平面;(Ⅱ)求二面角的正弦值;(Ⅲ)在棱上是否存在点使得平面?若存在,试求的值;若不存在,请说明理由.高中数学常见题型解法归纳及反馈检测第51讲:空间几何点的坐标的写法参考答案【反馈检测1答案】(1)证明过程详见解析;(2).【反馈检测1详细解析】如图建立空间...