高考数学 艺体生精选好题突围系列（基础篇）专题05 函数的基本性质-人教版高三全册数学试题VIP免费

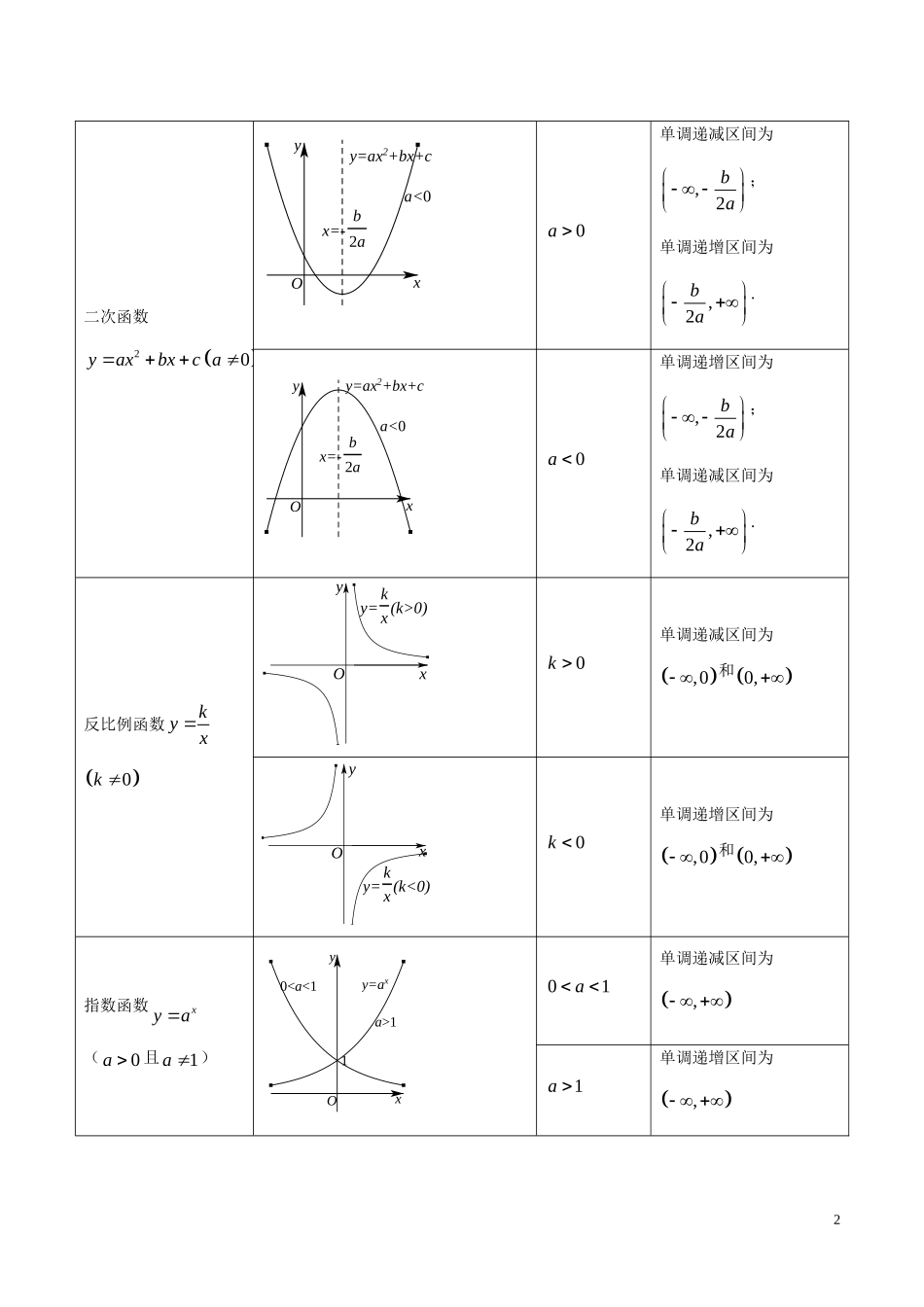
专题05函数的基本性质函数的单调性【背一背基础知识】1.单调区间：若函数fx在区间D上是增函数（或减函数），则称函数fx在区间D为单调递增（或单调递减），区间D叫做yfx的单调递增区间（或单调递减区间）；2.函数的单调性：设函数fx的定义域为I，如果对于定义域I内的某个区间D上任意两个自变量1x、2x，当12xx时，有12fxfx（或12fxfx），那么就说函数fx在区间D上是增函数（或减函数）；或对于区间D上任意两个自变量1x、2x，当12xx时，有12120fxfxxx或12120xxfxfx时，称函数fx在区间D上是增函数；或对于区间D上任意两个自变量1x、2x，当12xx时，有12120fxfxxx或12120xxfxfx时，称函数fx在区间D上是减函数.3.基本初等函数的单调性：函数图象参数范围单调区间或单调性一次函数0ykxbkk<0k>0Oyx0k单调递增区间,0k单调递减区间,1二次函数20yaxbxcaa<0x=-b2ay=ax2+bx+cOyx0a单调递减区间为,2ba；单调递增区间为,2ba.a<0x=-b2ay=ax2+bx+cOyx0a单调递增区间为,2ba；单调递减区间为,2ba.反比例函数kyx0kOyxy=kxk>0()0k单调递减区间为,0和0,Oyxy=kxk<0()0k单调递增区间为,0和0,指数函数xya（0a且1a）a>10101α=1α=011y=xαOyx0在0,上递减0没有单调性0在0,上递增正弦函数sinyxyx-11O-3π2-π2-π-2π3π2π2π2π单调递增区间2,222kk单调递减区间32,222kkkZ余弦函数cosyxOyx-11-32π32π-π2π2-2π2π-ππ单调递减区间2,2kk；单调递增区间2,2kkkZ3正切函数tanyxy-ππO-3π23π2-π2π2单调递增区间,22kkkZ【讲一讲基本技能】必备技能：1.在判断基本初等函数的单调性时，在熟悉基本初等函数的图象的基础上进行判断，尤其要注意，函数在区间D上的单调性和函数在区间D的子区间DDD上的单调性相同；在涉及若干个函数的和函数时，判断此函数的单调性一般利用性质去判断，即①增函数增函数增函数，②增函数减函数增函数，③减函数减函数减函数，④减函数增函数减函数；分段函数在定义域上的具有一种单调性，则要求分段函数在每段定义域上的单调性保持一致，还对断点处的函数值的大小有要求；一般情况下的单调性可利用导数求进行判断，即由0fx确定的解集为函数fx的单调递减区间，由0fx确定的解集为函数fx的单调递增区间；证明函数的单调性可以利用定义法与导数法.同时需要注意函数的同类单调区间（即同为增区间或减区间）不能取并集，一般利用逗号隔开或用“和”字联结.2.复合函数法：对于函数yfgx，可设内层函数为ugx，外层函数为yfu，可以利用复合函数法来进行求解，遵循“同增异减”，即内层函数与外层函数在区间D上的单调性相同，则函数yfgx在区间D上单调递增；内层函数与外层函数在区间D上的单调性相反，则函数yfgx在区间D上单调递减.3.导数法：不等式0fx的解集与函数fx的定义域的交集即为函数fx的单调递增区间，不等式0fx的解集与函数fx的定义域的交集即为函数fx的单调递减区间.【注】函数的多个递增区间或递减区间不能合并，在表示的时候一般将各区间用逗号或“和”字进行连接.4典型例题例1下列函数中,既是奇函数又是增函数的为（）A.1yxB.yxxC.1yxD.2yx分析：本题属于基本初等函数的单调性进行判断，判断...