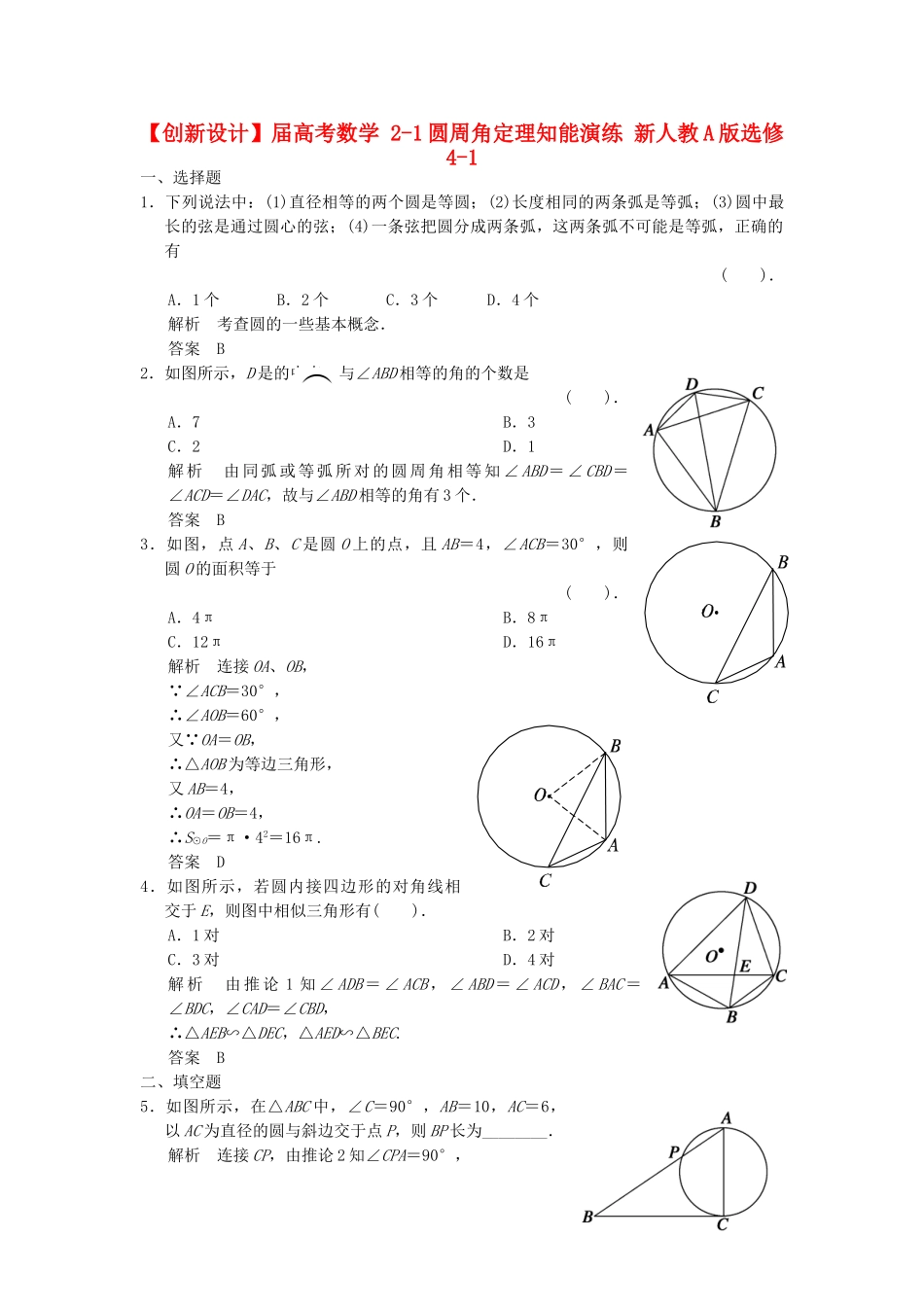
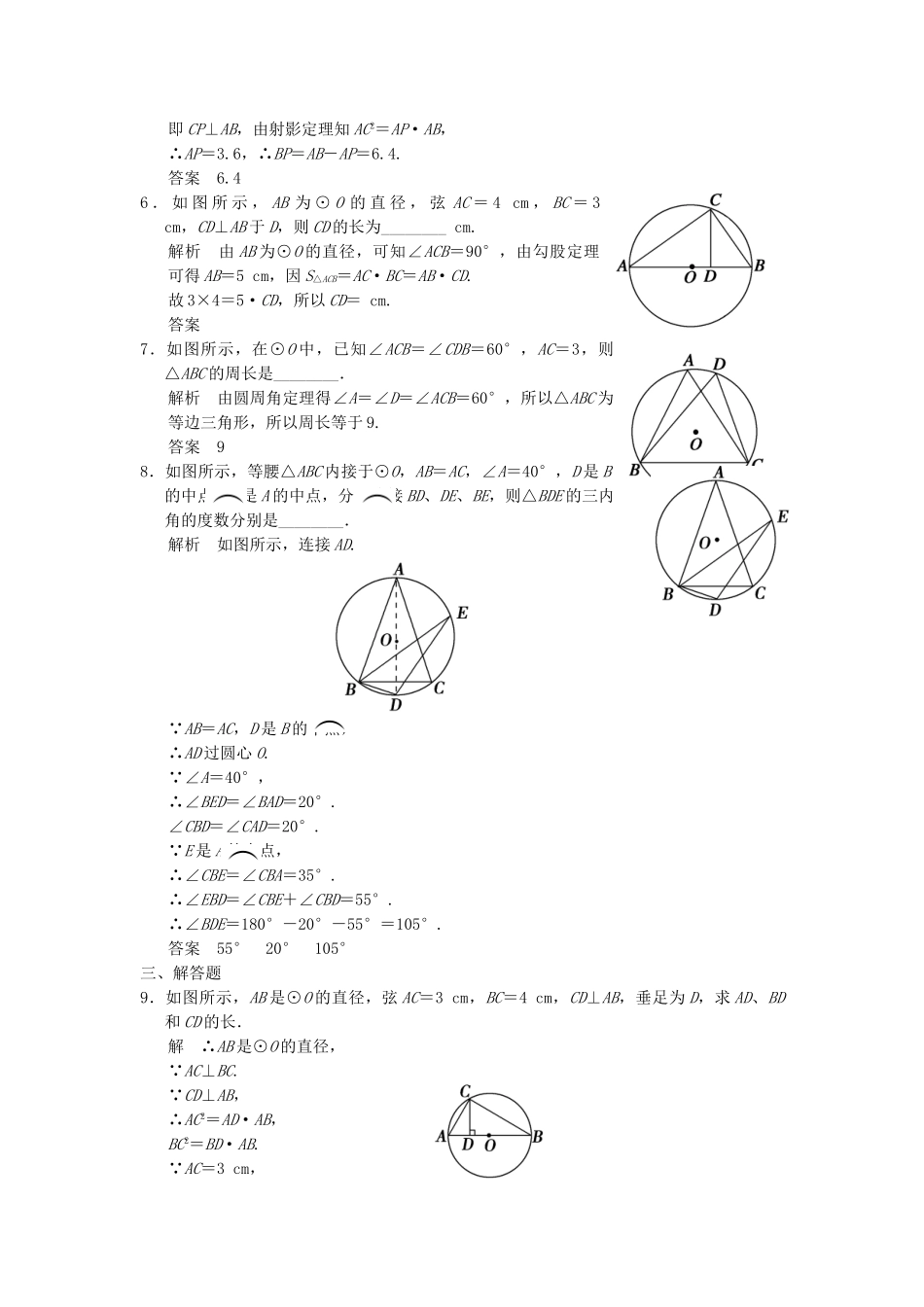
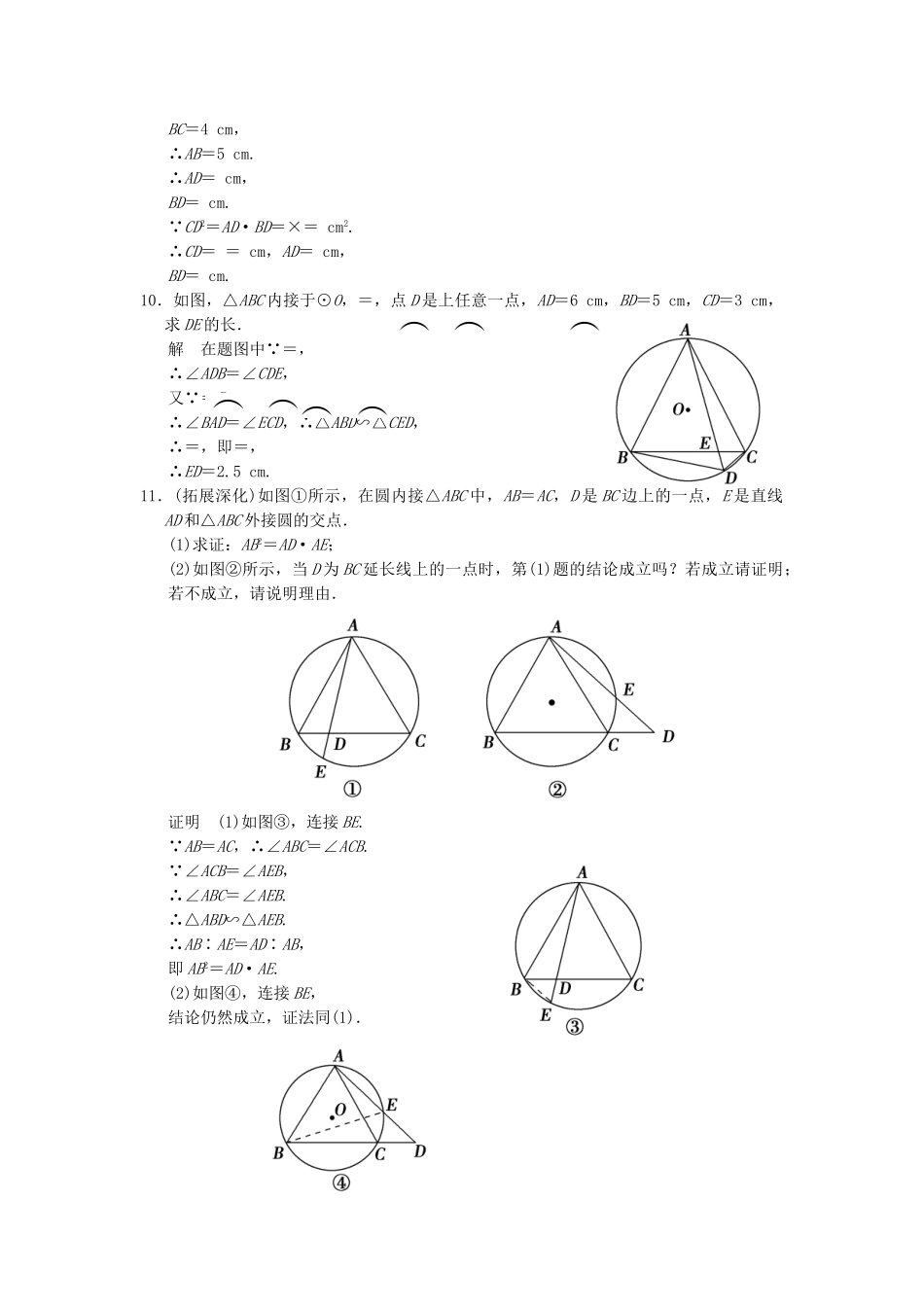
【创新设计】届高考数学2-1圆周角定理知能演练新人教A版选修4-1一、选择题1.下列说法中:(1)直径相等的两个圆是等圆;(2)长度相同的两条弧是等弧;(3)圆中最长的弦是通过圆心的弦;(4)一条弦把圆分成两条弧,这两条弧不可能是等弧,正确的有().A.1个B.2个C.3个D.4个解析考查圆的一些基本概念.答案B2.如图所示,D是的中点,与∠ABD相等的角的个数是().A.7B.3C.2D.1解析由同弧或等弧所对的圆周角相等知∠ABD=∠CBD=∠ACD=∠DAC,故与∠ABD相等的角有3个.答案B3.如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于().A.4πB.8πC.12πD.16π解析连接OA、OB,∵∠ACB=30°,∴∠AOB=60°,又∵OA=OB,∴△AOB为等边三角形,又AB=4,∴OA=OB=4,∴S⊙O=π·42=16π.答案D4.如图所示,若圆内接四边形的对角线相交于E,则图中相似三角形有().A.1对B.2对C.3对D.4对解析由推论1知∠ADB=∠ACB,∠ABD=∠ACD,∠BAC=∠BDC,∠CAD=∠CBD,∴△AEB∽△DEC,△AED∽△BEC.答案B二、填空题5.如图所示,在△ABC中,∠C=90°,AB=10,AC=6,以AC为直径的圆与斜边交于点P,则BP长为________.解析连接CP,由推论2知∠CPA=90°,即CP⊥AB,由射影定理知AC2=AP·AB,∴AP=3.6,∴BP=AB-AP=6.4.答案6.46.如图所示,AB为⊙O的直径,弦AC=4cm,BC=3cm,CD⊥AB于D,则CD的长为________cm.解析由AB为⊙O的直径,可知∠ACB=90°,由勾股定理可得AB=5cm,因S△ACB=AC·BC=AB·CD.故3×4=5·CD,所以CD=cm.答案7.如图所示,在⊙O中,已知∠ACB=∠CDB=60°,AC=3,则△ABC的周长是________.解析由圆周角定理得∠A=∠D=∠ACB=60°,所以△ABC为等边三角形,所以周长等于9.答案98.如图所示,等腰△ABC内接于⊙O,AB=AC,∠A=40°,D是B的中点,E是A的中点,分别连接BD、DE、BE,则△BDE的三内角的度数分别是________.解析如图所示,连接AD.∵AB=AC,D是B的中点,∴AD过圆心O.∵∠A=40°,∴∠BED=∠BAD=20°.∠CBD=∠CAD=20°.∵E是A的中点,∴∠CBE=∠CBA=35°.∴∠EBD=∠CBE+∠CBD=55°.∴∠BDE=180°-20°-55°=105°.答案55°20°105°三、解答题9.如图所示,AB是⊙O的直径,弦AC=3cm,BC=4cm,CD⊥AB,垂足为D,求AD、BD和CD的长.解∴AB是⊙O的直径,∵AC⊥BC.∵CD⊥AB,∴AC2=AD·AB,BC2=BD·AB.∵AC=3cm,BC=4cm,∴AB=5cm.∴AD=cm,BD=cm.∵CD2=AD·BD=×=cm2.∴CD==cm,AD=cm,BD=cm.10.如图,△ABC内接于⊙O,=,点D是上任意一点,AD=6cm,BD=5cm,CD=3cm,求DE的长.解在题图中∵=,∴∠ADB=∠CDE,又∵=B,∴∠BAD=∠ECD,∴△ABD∽△CED,∴=,即=,∴ED=2.5cm.11.(拓展深化)如图①所示,在圆内接△ABC中,AB=AC,D是BC边上的一点,E是直线AD和△ABC外接圆的交点.(1)求证:AB2=AD·AE;(2)如图②所示,当D为BC延长线上的一点时,第(1)题的结论成立吗?若成立请证明;若不成立,请说明理由.证明(1)如图③,连接BE.∵AB=AC,∴∠ABC=∠ACB.∵∠ACB=∠AEB,∴∠ABC=∠AEB.∴△ABD∽△AEB.∴AB∶AE=AD∶AB,即AB2=AD·AE.(2)如图④,连接BE,结论仍然成立,证法同(1).