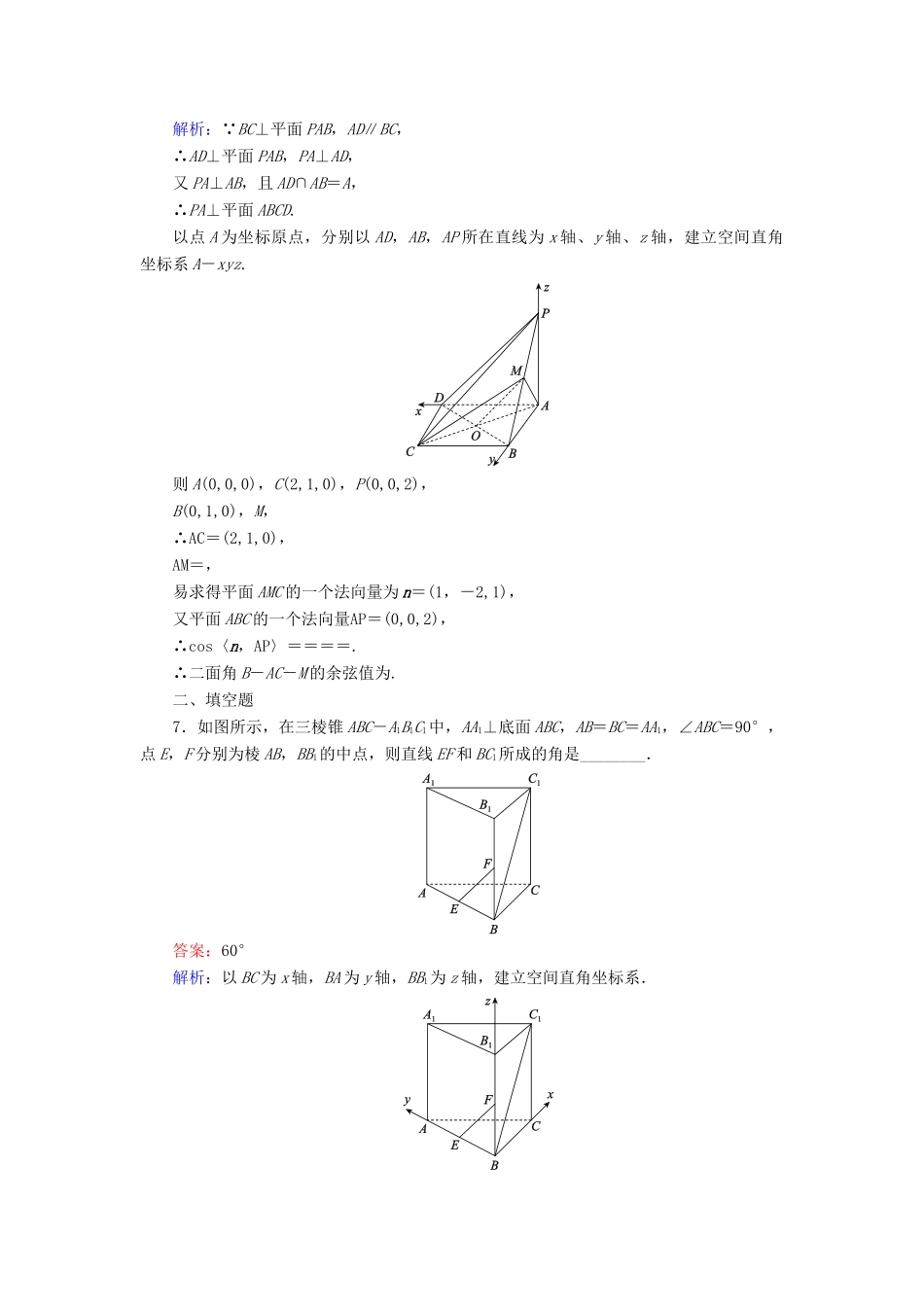
课时作业(四十六)立体几何中的向量方法一、选择题1.平面α的一个法向量为n=(1,2,0),平面β的一个法向量为m=(2,-1,0),则平面α和平面β的位置关系是()A.平行B.相交但不垂直C.垂直D.重合答案:C解析: n=(1,2,0),m=(2,-1,0),∴m·n=2-2+0=0,即m⊥n,∴α⊥β.2.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于()A.2B.-4C.4D.-2答案:C解析: α∥β,∴==,∴k=4.3.(2015·济南模拟)已知平面α内有一个点A(2,-1,2),α的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是()A.(1,-1,1)B.C.D.答案:B解析:对于选项A,PA=(1,0,1),则PA·n=(1,0,1)·(3,1,2)=5≠0,故排除A;对于选项B,PA=,则PA·n=·(3,1,2)=0,B正确;对于选项C,PA=,PA·n=·(3,1,2)=6≠0,C不正确;对于选项D,PA=,PA·n=·(3,1,2)=12≠0,D不正确.故应选B.4.如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=,AD=2,P为C1D1的中点,M为BC的中点,则AM与PM的位置关系为()A.平行B.异面C.垂直D.以上都不对答案:C解析:以点D为原点,分别以DA,DC,DD1所在直线为x,y,z轴,建立如图所示的空间直角坐标系D-xyz,依题意,可得D(0,0,0),P(0,1,),C(0,2,0),A(2,0,0),M(,2,0).∴PM=(,1,-),AM=(-,2,0),∴PM·AM=(,1,-)·(-,2,0)=0,即PM⊥AM,∴AM⊥PM.5.在正四面体P-ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为()A.B.aC.D.a答案:B解析:根据题意,可建立如图所示的空间直角坐标系P-xyz,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a).过点P作PH⊥平面ABC,交平面ABC于点H,则PH的长即为点P到平面ABC的距离. PA=PB=PC,∴H为△ABC的外心.又 △ABC为正三角形,∴H为△ABC的重心,可得H点的坐标为.∴PH==a.∴点P到平面ABC的距离为a.6.(2015·昆明模拟)如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,且BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2.若AB=1,则二面角B-AC-M的余弦值为()A.B.C.D.答案:A解析: BC⊥平面PAB,AD∥BC,∴AD⊥平面PAB,PA⊥AD,又PA⊥AB,且AD∩AB=A,∴PA⊥平面ABCD.以点A为坐标原点,分别以AD,AB,AP所在直线为x轴、y轴、z轴,建立空间直角坐标系A-xyz.则A(0,0,0),C(2,1,0),P(0,0,2),B(0,1,0),M,∴AC=(2,1,0),AM=,易求得平面AMC的一个法向量为n=(1,-2,1),又平面ABC的一个法向量AP=(0,0,2),∴cos〈n,AP〉====.∴二面角B-AC-M的余弦值为.二、填空题7.如图所示,在三棱锥ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别为棱AB,BB1的中点,则直线EF和BC1所成的角是________.答案:60°解析:以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系.设AB=BC=AA1=2,则C1(2,0,2),E(0,1,0),F(0,0,1),则EF=(0,-1,1),BC1=(2,0,2),∴EF·BC1=2,∴cos〈EF,BC1〉==,∴EF和BC1所成的角为60°.8.如图,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是________.答案:平行解析: 正方体棱长为a,A1M=AN=,∴MB=A1B,CN=CA,∴MN=MB+BC+CN=A1B+BC+CA=(A1B1+B1B)+BC+(CD+DA)=B1B+B1C1.又 CD是平面B1BCC1的法向量,∴MN·CD=·CD=0,∴MN⊥CD.又 MN⊄平面B1BCC1,∴MN∥平面B1BCC1.9.设正方体ABCD-A1B1C1D1的棱长为2,则点D1到平面A1BD的距离是________.答案:解析:如图,建立空间直角坐标系,则D1(0,0,2),A1(2,0,2),D(0,0,0),B(2,2,0),∴D1A1=(2,0,0),DA1=(2,0,2),DB=(2,2,0),设平面A1BD的一个法向量为n=(x,y,z),则令x=1,则n=(1,-1,-1),∴点D1到平面A1BD的距离d===.三、解答题10.(2015·济南一模)如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=,M为棱PB的中点.(1)证明:DM⊥平面PBC;(2)求二面角A-DM-C的余弦值.解:(1)证明:连接BD,取DC的中点G,连接BG,由此知DG=GC=BG=1,即△DBC为直角三角形,...