安徽省安庆市高三数学第一学期期末教学质量监测试卷 理试卷VIP免费

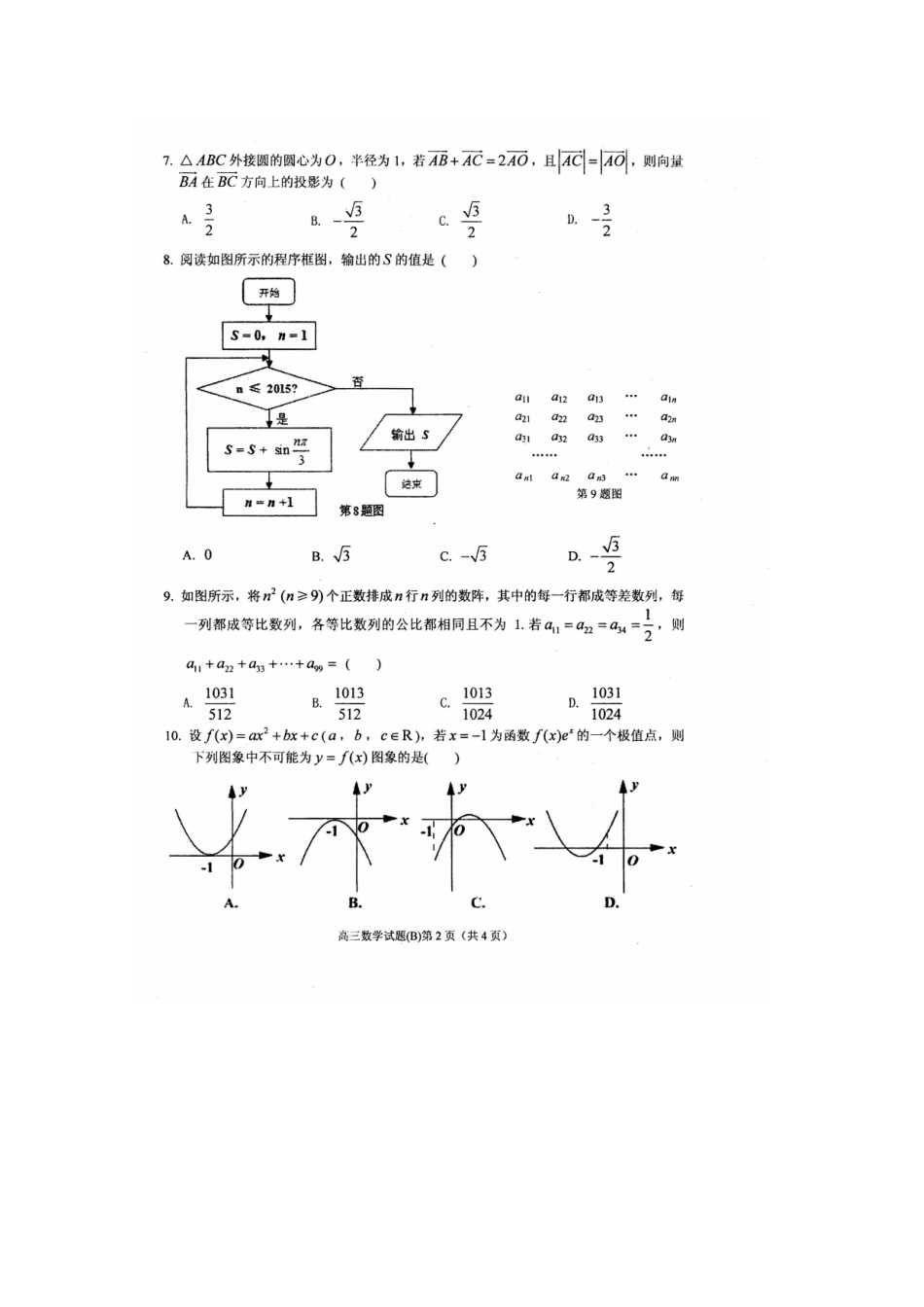
安徽省安庆市2014～2015学年度第一学期期末教学质量调研监测理科数学安庆市2014～2015学年度第一学期期末教学质量调研监测高三数学试题（B）参考答案及评分标准一、选择题1.C2.B【解析】(3.5)(2.51)(2.5)(1.51)(1.5)(0.51)ffffff(0.5)0.5f.3.D【解析】242pp.4.C5.C6.B【解析】因为26nm，24qp，所以22266644nmmqpp.7.A20ABACAOABAOACAOOBOC�，所以BC为圆O的直径.又1ACAO�，所以∠60C°，∠30B°，3BA�，所以向量BA�在BC�方向上的投影为3cos2BAB�.8.A【解析】232015sinsinsinsin03333S.9.B【解析】设公比为q，因为11223412aaa，则2112aq，23112aq，3212aq.由31a，32a，33a，34a成等差数列，有343132313()aaaa，得1q（舍）或12q.所以121a，1111211(1)()2nnaanaa，11222nnnnnna，所以1122339923912392222aaaa，由错位相减法可得112233991013512aaaa.10.D【解析】由1x为函数()xfxe的一个极值点可得ac，∴2()fxaxbxa.若()fx有两个零点1x，2x，则121xx，显然D不适合.二、填空题11.若0x且0y，则0xy.12.913.214.27【解析】由2sinsinsinacbACB，得2sinaA，2sincC，所以24sin2sin4sin2sin(120)5sin3cosacACAAAA，所以2ac的最大值为25327.15①③④【解析】作出两个函数的图象.三、解答题16.【解析】（1）211()cos3sincos22fxabxxx131(1cos2)sin2cos22223xxx.因为直线3x是()yfx图象的一条对称轴，所以233k，31()2kkz，当1k时，正数取得最小值1.………6分（2）当1时，()cos23fxx.由2223kxk≤≤，得236kxk≤≤.所以()fx的单调增区间236kk，(Zk).…………12分17.【解析】（1）取1AA中点D，连接BD、1CD、1AC，因为11ABABAA，所以△1ABA是正三角形，所以1BDAA.根据侧面11ABBA⊥侧面11ACCA，有BD⊥侧面11ACCA.由12AAAC，平行四边形11ACCA的面积为23，∠11AAC为锐角，可得∠1160AAC°，所以△11AAC为正三角形，有11CDAA.所以1AA平面1BCD，从而1AA⊥1BC.…………6分（2）因为112ABABAA，所以3BD，所以四棱锥11BAACC的体积为123323V.又三棱锥111BABC的体积为三棱柱111ABCABC体积的13，所以四棱锥11BAACC的体积为三棱柱111ABCABC体积的23.从而所求的斜三棱柱111ABCABC的体积为3.…………12分18.【解析】（1）甲答错题目数的平均数为32011.54x，所以答对题目数的平均数为101.58.5，所以甲第一卷的平均得分为8.5542.5.…………6分（2）根据题意知点()Pxy，共有16个：(34)，、(33)，、(32)，、(30)，、(24)，、(23)，、(22)，、(20)，、(04)，、(03)，、(02)，、(00)，、(14)，、(13)，、(12)，和(10)，.因为2221ykyxx≥≥，所以符合2k≥的点P共有8个：(24)，、(04)，、(03)，、(02)，、(10)，、(12)，、(13)，、(14)，.故所求的概率为81P162.…………12分19.【解析】（1）由2211112(2)()0nnnnnnnnaaaaaaaa.因为0na，*Nn，所以120nnaa，即12nnaa，所以数列{}na是首项为2，公比为2的等比数列.故2nna，*Nn.…………5分（2）22(1)(1)(12)(12)nnnnnbaaaa.1nnbb，即1212(12)(12)(12)(12)nnnnaa，化简得232na.因为2322324n≤，所以4a时，有1nnbb.…………12分20.【解析】（1）由直线32yx与圆222xyb相切，得1b.由32ca，222abc，得2a.所以椭圆C的方程为2214xy.…………5分（2）设11()Pxy，，22()Txy，，12xx，则直线PT的方程为122212()yyyyxxxx.令0y，得122112221212xxxyxyxxyyyyy，所以211212xyxyOMyy...