高中数学 142正弦函数、余弦函数的性质(2)课件 新人教A版必修4 课件VIP免费

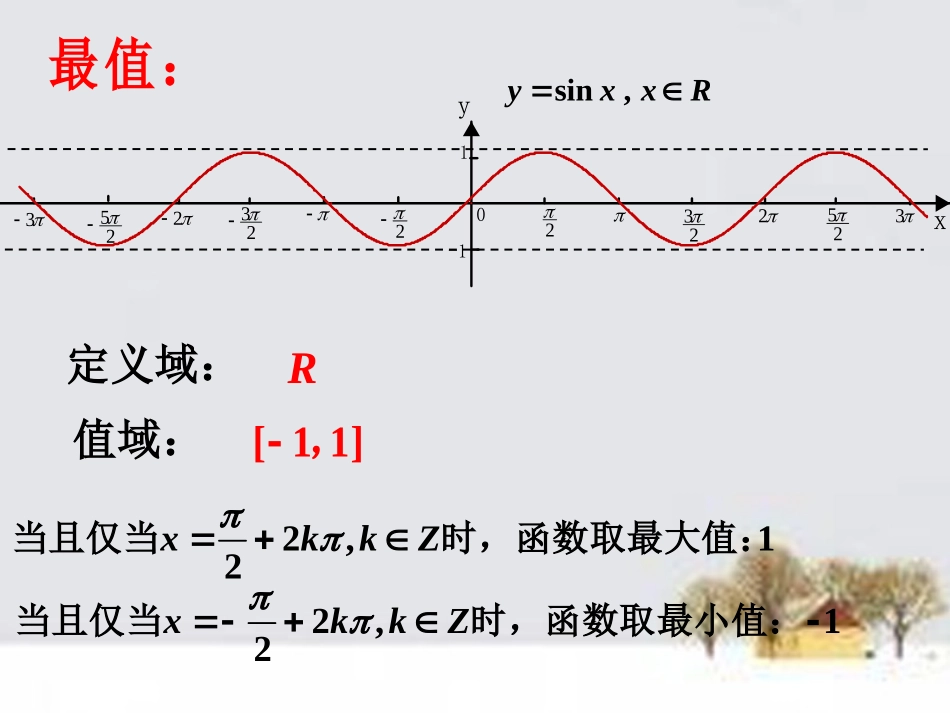
1.4.2正弦函数、余弦函数的性质（2）定义域：R值域：[11]，2,12xkkZ当且仅当时，函数取最大值：2,12xkkZ当且仅当时，函数取最小值：-32532522322322-11yx0sin,yxxR最值：2o46246xy---------1-1sinyx单调递增区间：[2,2],()22kkkZ单调递减区间：3[2,2],()22kkkZ单调性：()sinfxx奇偶性：()sin()fxxsin()xfx32532522322322-11yx0对称中心：(k,0),(kZ)对称中心：2o46246xy---------1-1思考：为什么图象是关于这些点中心对称呢？()sinfxx2o46246xy---------1-1,()2xkkZ对称轴：()sinfxx思考：为什么图象是关于这些直线轴对称呢？对称轴：正弦函数的图象性质:(1)定义域(2)值域R.[-1，1].当且仅当时取得最大值1，当且仅当时取得最小值-1.Zkkx，22Zkkx，22(3)奇偶性奇函数.(5)单调性增区间减区间Zkkk22,22Zkkk223,22(6)对称性:图象关于直线轴对称，关于点中心对称.Zkkx，2Zkk，，)0((4)周期性周期函数,Rxxy，sin32532522322322-11yx02Tk(0)kZk且余弦函数的图象性质:(1)定义域(2)值域R.[-1，1].当且仅当时取得最大值1，当且仅当时取得最小值-1.Zkkx，2Zkkx，)12((3)奇偶性偶函数.(5)单调性增区间减区间(6)对称性:图象关于直线轴对称，关于点中心对称.Zkkx，Zkk，，)02(Zkkk2)12(，Zkkk)12(2，(4)周期性周期函数,32532522322322-11yx0Rxxy，cos2Tk(0)kZk且例1.求下列函数的最大值，并求出最大值时x的集合：，）（1cos1xyR.x2sin2yx（），R.x3sin.yaxb（）解：1cos1x（）当2()xkkZ，即时，y取得最大值max2.y∴函数的最大值为2，取最大值时的x集合为2Zxxkk，(2)sin21x当，222xk即()4xkkZ时，y取得最大值max1.yZ4xxkk，∴函数的最大值为1，取最大值时的x集合为3sin.yaxb（）解：0a若，sin1x则当时，函数取得最大值max.yab．0a若，yb则，此时函数为常数函数，0a若，sin1x则当时，函数取得最大值max.yab①2Z.2xxkk此时，②③函数最大值2Z.2xxkk此时，max.yb.xxR此时注意：对于含参数的最大值或最小值问题，要对sinx或cosx的系数进行讨论．思考：此例若改为求最小值，结果如何？例2比较下列各组数的大小：(1)sin()sin()1810与；2317(2)cos()cos()54与；4321(3)cossin().95与解：(1)sin[]21018222yxx，且，，是增函数，sin()sin().181023(2)cos()523cos517cos()417cos43cos(4)53cos5，1cos(4)41cos.4130cos[0]45yxx又，且，，是减函数，3cos51cos4，2317cos()cos().54即4321(3)cossin().95与43cos97cos(4)97cos921sin()51sin(4)51sin52cos()92cos9，2cos9又2sin()295sin185sin[]2518222yxx而，且，，是增函数，5sin181sin52cos9即1sin52cos91sin5，4321cossin().95即解：课后作业1.教材第46页习题1.4A组2~52.《乐学》蓝皮1.4.1、1.4.2剩余题目