高三数学一轮复习 第3章3.2同角三角函数的基本关系及诱导公式课件 文 北师大版 课件VIP免费

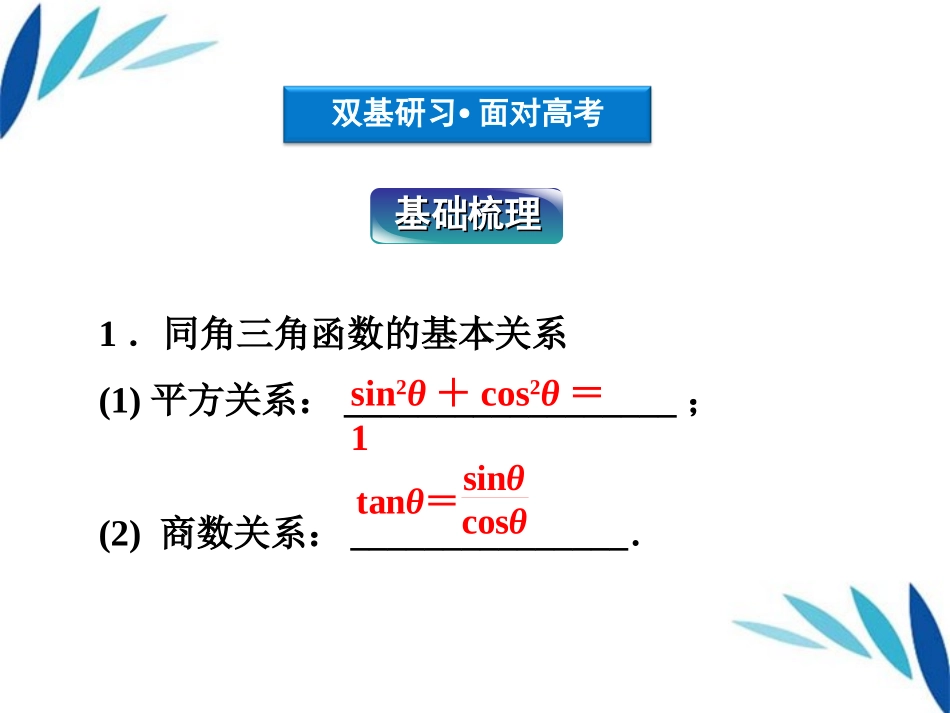
§3.2同角三角函数的基本关系及诱导公式考点探究•挑战高考考向瞭望•把脉高考§3.2同角三角函数的基本关系及诱导公式双基研习•面对高考双基研习•面对高考基础梳理基础梳理1．同角三角函数的基本关系(1)平方关系：__________________；(2)商数关系：_______________.sin2θ＋cos2θ＝1tanθ＝sinθcosθ2．诱导公式函数角正弦余弦正切α＋k·2π(k∈Z)sinαcosα_______α＋π－sinα_______tanα－α______cosα－tanα2π－α－sinα______－tanαπ－α______－cosα______＋αcosα_______－α_______sinαπ2π2tanα－cosα－sinαcosαsinα－tanα－sinαcosα思考感悟如何利用上表中的诱导公式实现正弦函数与余弦函数的相互转化？提示：利用公式“±α”可实现正弦函数与余弦函数的相互转化．总口诀为：奇变偶不变，符号看象限，其中“奇、偶”是指“k·π2±α(k∈Z)”中k的奇偶性；“符号”是把任意角α看作锐角时，原函数值的符号．答案：D课前热身1．cos585°等于()A．－32B.32C.22D．－22答案：A2．(教材习题改编)sin(5π2＋π4)＋sin(－55π6)的值是()A.2＋12B.2－12C.1－22D．－2＋12答案：D3．(2009年高考全国卷Ⅱ)已知ΔABC中，1tanA＝－125，则cosA等于()A.1213B.513C．－513D．－12135．sin21°＋sin22°＋sin23°＋…＋sin288°＋sin289°的值为________．4．(2011年济源质检)cos(－796π)的值为________．答案：－32答案：4412考点探究•挑战高考考点突破考点突破三角函数式的化简利用诱导公式、同角三角函数的基本关系式进行化简时，一般多直接应用公式，在此情况下容易出错的地方是三角函数的符号．【思路点拨】观察分析每一个角(式)，看其是否能直接使用公式，不能直接使用，要对其进行合理变形．化简下列各式．(1)1＋sinα1－sinα－1－sinα1＋sinα(α是第三象限角)；(2)1－2sin40°cos40°；(3)sin2α＋sin2β－sin2αsin2β＋cos2αcos2β；(4)tanπ－αcos2π－αsin－α＋3π2cos－α－πsin－π－α.例例11【解】(1)原式＝1＋sinα1＋sinα1－sinα1＋sinα－1－sinα1－sinα1＋sinα1－sinα＝1＋sinα21－sin2α－1－sinα21－sin2α＝1＋sinα|cosα|－1－sinα|cosα|， α是第三象限角，∴cosα<0，∴原式＝1＋sinα－cosα－1－sinα－cosα＝－2tanα.(2)1－2sin40°cos40°＝sin40°－cos40°2＝|sin40°－cos40°|. sin40°0，求cosθ的值．例例22【解】(1) cos(－80°)＝cos80°＝k，∴sin80°＝1－cos280°＝1－k2，∴tan100°＝tan(180°－80°)，＝－tan80°＝－sin80°cos80°＝－1－k2k.(2)由tanθ＝sinθcosθ>0，知sinθ与cosθ同号，∴cosθ＝－1－sin2θ＝－1－－452＝－35.【误区警示】利用sin2θ＋cos...