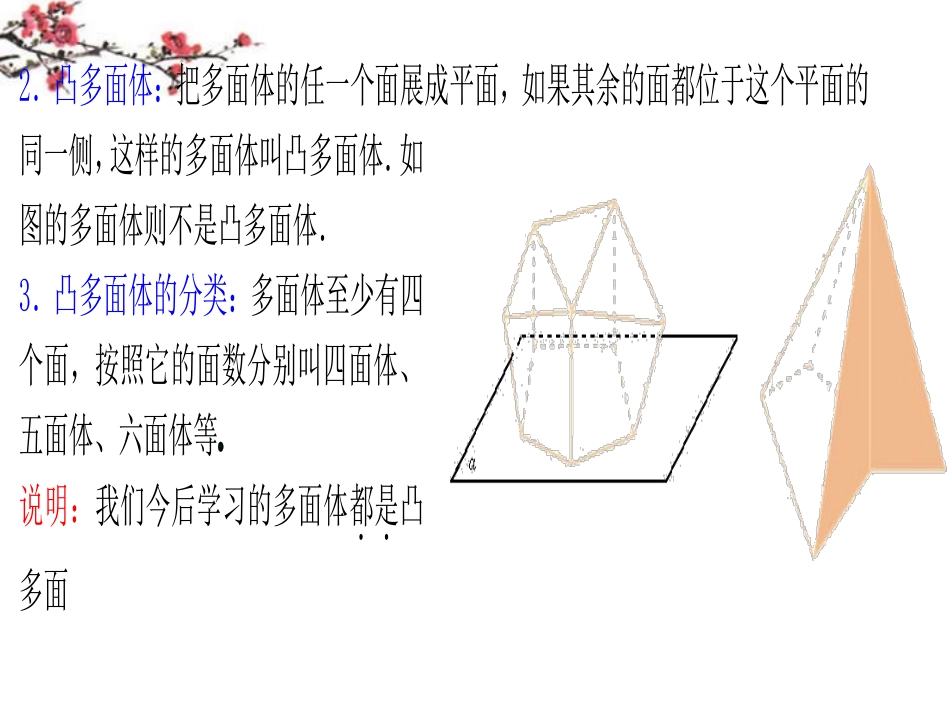
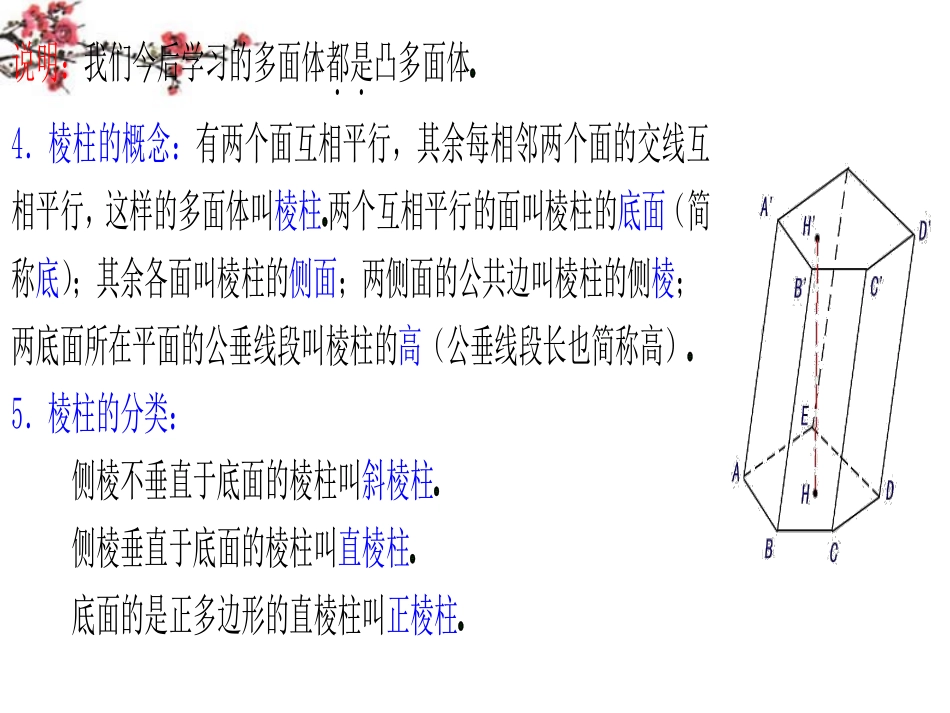
一、复习引入:从一些常见的物体(凸多面体),例如三棱镜,方砖等,它们呈棱柱的形状(如图)奎屯王新敞新疆二、讲解新课:1奎屯王新敞新疆多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线.2.凸多面体:把多面体的任一个面展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫凸多面体.如图的多面体则不是凸多面体.3.凸多面体的分类:多面体至少有四个面,按照它的面数分别叫四面体、五面体、六面体等奎屯王新敞新疆说明:我们今后学习的多面体都是..凸多面说明:我们今后学习的多面体都是..凸多面体奎屯王新敞新疆4.棱柱的概念:有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱奎屯王新敞新疆两个互相平行的面叫棱柱的底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高)奎屯王新敞新疆5.棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱奎屯王新敞新疆侧棱垂直于底面的棱柱叫直棱柱奎屯王新敞新疆底面的是正多边形的直棱柱叫正棱柱奎屯王新敞新疆设集合{}A棱柱,{}B斜棱柱,{}C直棱柱,{}D正棱柱,则,BCADC.棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……6.棱柱的性质(1)棱柱的侧棱相等,侧面都是平行四边形;直棱柱侧面都是矩形;正棱柱侧面都是全等的矩形;(2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等的多边形(图(1));(3)过棱柱不相邻的两条侧棱的截面都是平行四边形(图(2)).棱柱的概念有两个本质的属性:①有两个面(底面)互相平行;②其余每相邻两个面的交线互相平行.要注意“有两个面互相平行,其余各面都是平行四边形的多面体”不一定是棱柱.三、讲解范例:例1奎屯王新敞新疆已知正三棱柱ABCABC的各棱长都为1,M是底面上BC边的中点,N是侧棱CC上的点,且14CNCC,求证:ABMN.证明(法一):设ABa�,ACb�,AAc�,则||||||1abc,1,0aaacbc,ABac�,1()2AMac�,14ANbc�,111224MNANAMabc�,111()()224ABMNacabc�111cos600224,∴ABMN.M'MB'C'A'CBAxyz(法二):取BC的中点M,∴//MMBB,又∵BB底面ABC,∴MM底面ABC,∵ABC是正三角形,M是BC边的中点,∴AMBC,分别以,,MCMAMM为x轴、y轴、z轴建立空间直角坐标系,则11(,0,)24MN�,3(0,,0)2A,1(,0,1)2B,13(,,1)22AB�,1131()0()102224ABMN�.∴ABMN.GFEDC'B'A'CBA例2.正三棱柱ABCABC的底边长为a的正三角形,在侧棱BB上截取2aBD,在侧棱CC上截取CEa,(1)求证:平面ADE平面ACCA;(2)求ADE的面积奎屯王新敞新疆证明:(1)分别取,AEAC中点,FG,连结,,DFFGBG,则1//,2FGECFGEC,又∵1//,2DBECDBEC,//,FGDBFGDB,∴四边形DFGB是平行四边形,∴//DFBG,∵ABC是正三角形,∴BGAC,又平面ABC平面ACCA,BG平面ACCA,∴DF平面ACCA,又∵DF平面ADE,∴平面ADE平面ACCA.(2)在直角梯形BDEC中,225()2DEECDBBCa,在直角三角形DBA中,2252DADBABa,在直角三角形ECA中,222AEECACa,∴2232DFDEEFa,∴21624ADESAEDFa