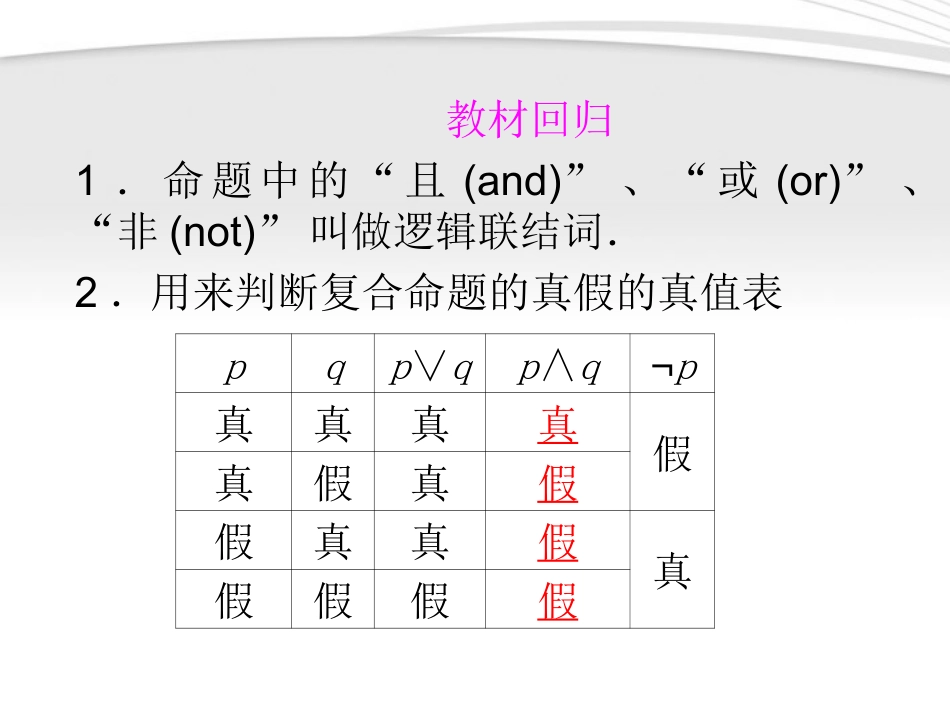
考纲定位1.简单的逻辑联结词了解逻辑联结词“或”、“且”、“非”的含义.2.全称量词与存在量词(1)理解全称量词与存在量词的意义(2)能正确地对含有一个量词的命题进行否定.教材回归1.命题中的“且(and)”、“或(or)”、“非(not)”叫做逻辑联结词.2.用来判断复合命题的真假的真值表pqp∨qp∧q¬p真真真真假真假真假假真真假真假假假假3.全称量词(universalquantifier)与存在量词(existentialquantifier)(1)常见的全称量词有:“任意一个”、“一切”、“每一个”、“任给”、“所有的”等.(2)常见的存在量词有:“存在一个”、“至少有一个”、“有些”、“有一个”、“某个”、“有的”等.(3)全称量词用符号“∀”表示;存在量词用符号“∃”表示.4.全称命题与特称命题(1)含有全称量词的命题叫全称命题.(2)含有存在量词的命题叫特称命题.5.命题的否定(1)全称命题的否定是特称命题;特称命题的否定是全称命题.(2)p或q的否定为:非p且非q;p且q的否定为:非p或非q.三基强化1.命题“存在x0∈R,2x0≤0”的否定是()A.不存在x0∈R,2x0>0B.存在x0∈R,2x0≥0C.对任意的x∈R,2x≤0D.对任意的x∈R,2x>0解析:命题“存在x0∈R,2x0≤0”为一特称命题,因此它的否定是全称命题“对任意的x∈R,2x>0”,故选D.答案:D2.(2011年湖北八校)已知命题p:∃x∈R,使sinx=52;命题q:∀x∈R,都有x2+x+1>0.给出下列结论:①命题“p∧q”是真命题②命题“p∧¬q”是假命题③命题“¬p∨q”是真命题④命题“¬p∨¬q”是假命题其中正确的是()A.②③B.②④C.③④D.①②③解析: p假q真,∴¬q假,¬p真,∴p∧¬q假,¬p∨q真,故选A.答案:A3.(2010年辽宁辽阳模拟)如果命题“¬(p或q)”为假命题,则()A.p,q均为真命题B.p,q均为假命题C.p,q中至少有一个为真命题D.p,q中至多有一个为真命题解析:由题意知p或q为真命题,∴p、q中至少有一个为真命题,故选C.答案:C答案:C4.若函数f(x)=x2+ax(a∈R),则下列结论正确的是()A.∀a∈R,f(x)在(0,+∞)上是增函数B.∀a∈R,f(x)在(0,+∞)上是减函数C.∃a∈R,f(x)是偶函数D.∃a∈R,f(x)是奇函数解析:f′(x)=2x-ax2,故只有当a≤0时,f(x)在(0,+∞)上是增函数,因此A、B不对,当a=0时,f(x)=x2是偶函数,因此C对,D不对.5.下列命题的否定错误的是()A.p:能被3整除的数是奇数;¬p:存在一个能被3整除的数不是奇数B.p:任意四边形的四个顶点共圆;¬p:存在一个四边形的四个顶点不共圆C.p:有的三角形是正三角形;¬p:所有的三角形都不是正三角形D.p:∃x∈R,x2+2x+2≤0,¬p:当x2+2x+2>0时,x∈R答案:D考点一用“或”、“且”、“非”联结简单命题并判断其真假1.判断含有逻辑联结词的命题真假的关键是对逻辑联结词“或”、“且”、“非”含义的理解.数学中的逻辑联结词“或”与日常生活中的“或”意义不同,日常生活中的“或”带有不能同时具备之意.数学中的逻辑联结词“且”与日常生活中的“且”意义基本一致,表示而且的意思.数学中的逻辑联结词“非”与日常生活中的“非”意义基本一致,表示否定的意思.2.“p∨q”、“p∧q”、“¬p”形式命题真假的判断步骤:(1)确定命题的构成形式;(2)判断其中命题p、q的真假;(3)确定“p∨q”、“p∧q”、“¬p”形式命题的真假.【分析】先确定组成复合命题的每个简单命题的真假,再根据真值表判断复合命题的真假.例1判断下列命题的真假.(1)2属于集合Q,也属于集合R;(2)矩形的对角线互相垂直或相等;(3)不等式|x+2|≤0没有实数解.【解】(1)此命题为“p∧q”的形式,其中p:2∈Q,q:2∈R,因命题p为假命题,命题q为真命题,所以命题“p∧q”为假命题.故原命题为假命题.(2)此命题为“p∨q”的形式,其中p:矩形的对角线互相垂直,q:矩形的对角线相等,因命题p为假命题,命题q为真命题,所以p∨q为真命题.故原命题为真命题.(3)此命题是“¬p”的形式,其中p:不等式|x+2|≤0有实数解.因为x=-2是该不等式的一个解,所以命题p为真命题,即¬p为假命题.所以原命题为假命题.变式迁移1分别指出由下列命题构成的“p∨q”“p∧q”“¬...