棱柱的侧面积和体积 高二数学棱柱全套课件(含flash)人教版 高二数学棱柱全套课件(含flash)人教版VIP免费

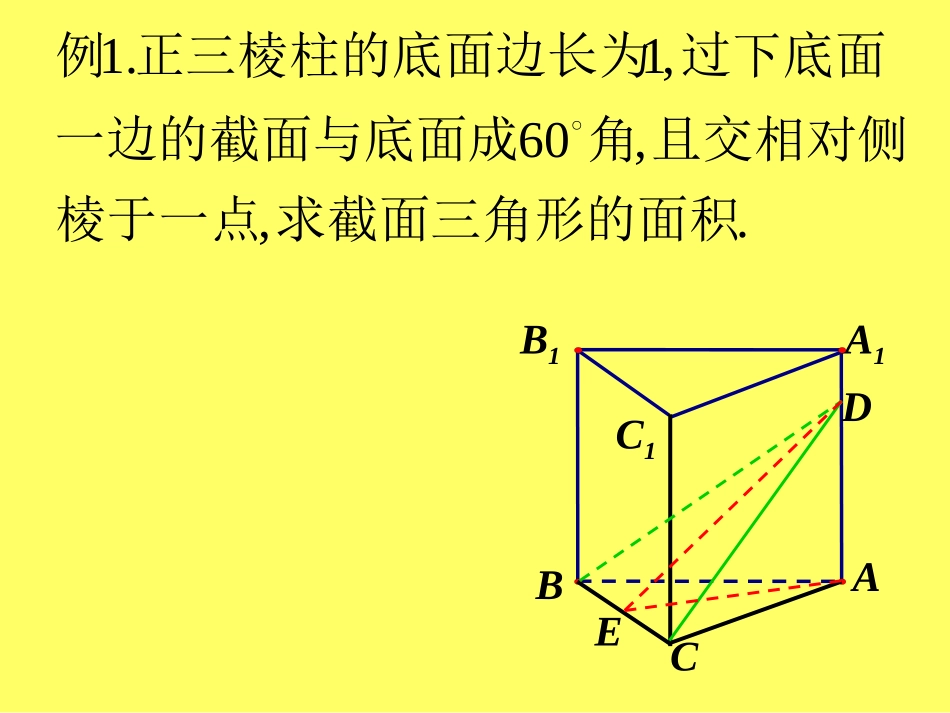
.,,60,1.1求截面三角形的面积棱于一点且交相对侧角一边的截面与底面成过下底面正三棱柱的底面边长为例A1C1BCAB1DE棱柱的侧面积:把棱柱的侧面沿一条侧棱剪开后展在一个平面上，展开图的面积就是棱柱的侧面积．棱柱的侧面积是指所有侧面面积之和直棱柱的展开图右图是直六棱柱的展开图。直棱柱的侧面展开图是矩形，由矩形面积的计算公式可得到侧面积的计算公式。1.如果直棱柱的底面周长是c，高是h，那么它的侧面积是S＝ch．hSV3.直棱柱的体积hcS直棱柱2.棱柱的表面积或全面积等于侧面积与底面积的和。1.若正方体的对角线长为3，则它的体积为[]2.已知一正方体的对角线长为a，那么这个正方体的表面积是[]3.长方体的一个顶点处的三个面的面积分别是2cm2、3cm2、6cm2,求它的体积？例2.直三棱柱底面各边的比为3∶4∶5，侧棱长为16,全面积为1440,求底面各边之长和体积.A1C1BCAB1练习:直三棱柱底面各边的比为17109∶∶，侧棱长为16cm,全面积为1440cm2,求底面各边之长.A1C1BCAB11：斜棱柱的侧面积LC直截面的周长侧棱长斜棱柱S底面面积高斜棱柱V2。棱柱的体积直截面的面积侧棱长斜棱柱V各个侧面面积之和斜棱柱S斜棱柱例3.斜三棱柱ABC—A1B1C1中，底面是边长为4的正三角形，且∠A1AB=∠A1AC=60°,AA1=8,求它的全面积.解:∵∠A1AB=∠A1AC=60°,∴AA1在底面ABC上的射影是∠BAC的平分线AD.∵△ABC为正三角形，∴AD⊥BC∴BC⊥AA1（三垂线定理）∴BC⊥BB1∴侧面BCC1B1是矩形各个侧面面积之和斜棱柱S例3.斜三棱柱ABC—A1B1C1中，底面是边长为4的正三角形，且∠A1AB=∠A1AC=60°,AA1=8,求它的全面积.另解:作BD⊥AA1于D，连结CD.∵∠A1AB=∠A1AC=60°△ABC是边长为4的正三角形，∴△ABD≌△ACD∴∠CDA=∠BDA=90°∵AA1⊥BD,AA1⊥CD∴AA1⊥截面BDC，平面BDC为直截面直截面的周长侧棱长斜棱柱S例4：如图，斜三棱柱ABC－A1B1C1的一个侧面面积为10，这个侧面与它所对棱的距离为6，求棱柱的体积。AA1B1BCC1PRQO直截面的面积侧棱长斜棱柱V解法一：沿斜三棱柱ABC—A1B1C1的侧面BB1C1C的面积为S，A1A和面BB1C1C的距离为6,在AA1上取一点P作直截面PQR，则AA1⊥截面PQR，AA1⊥RQ，∴截面PQR⊥侧面BB1C1C，过P作PO⊥QR于O，则PO⊥侧面BB1C1C，且PO=6.212121∴V斜=S△PQR·AA1＝·QR·PO·AA1＝·PO·QR·BB1＝×10×6=30.例4：如图，斜三棱柱ABC－A1B1C1的一个侧面面积为10，这个侧面与它所对棱的距离为6，求棱柱的体积。解法二：将斜三棱柱补成平行六面体ABCD—A1B1C1D1，因为三棱柱ABC—A1B1C1与三棱柱ACD—A1C1D1等底等高.,111111DCAACDCBAABCVV三棱柱三棱柱面AA1D1D到面BB1C1C的距离就是AA1到BB1C1C的距离.因此平面六面体BB1C1C—AA1D1D的底面积为10，高为6,所以V平行六面体＝60，∴21111CBAABCV三棱柱×60=30.补体法1：如果直棱柱的底面周长是c，高是h，那么它的侧面积是S＝ch．hSV2.直棱柱的体积直棱柱1：斜棱柱的侧面积直截面的周长侧棱长斜棱柱S底面面积高斜棱柱V2。棱柱的体积直截面的面积侧棱长斜棱柱V各个侧面面积之和斜棱柱S斜棱柱1.长方体长、宽、高的和为14,对角线长为8,则它的全面积为()A.64B.196C.132D.1282.正六棱柱的底面边长为4,高为12,则它的全面积为()288348C3.已知直三棱柱ABC－A1B1C1，侧棱AA1=4，它的底面△ABC中有AC=BC=2，∠C=90°，E是AB的中点．(1)求证：CE⊥AB1(2)求截面ACB1和侧面ABB1A1所成角的大小．H练习4:在三棱柱ABC－A1B1C1中，aAB2BC=CA=AA1=a，A1在底面的射影O恰为AC的中点，求：(1)AB与侧面AC1所成的角；(2)侧面AA1B1B和侧面CC1A1A所成的角；(3)三棱柱的侧面积和体积．