高三数学函数的极限函数的连续性 课件VIP免费

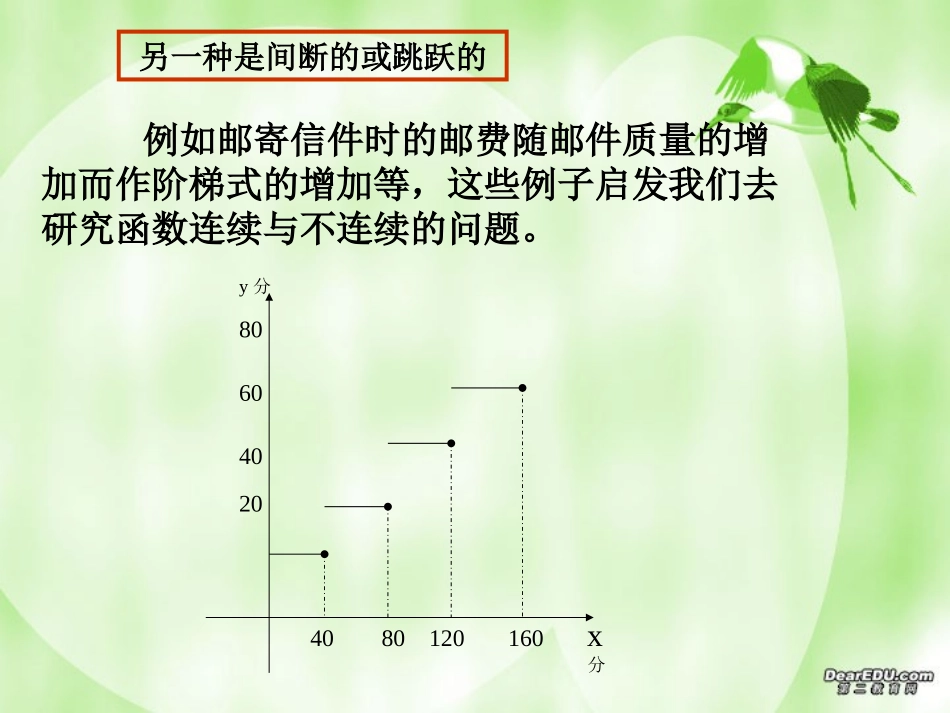
函数的连续性一种是连续变化的情况温度计4080120160x分y分20406080例如邮寄信件时的邮费随邮件质量的增加而作阶梯式的增加等，这些例子启发我们去研究函数连续与不连续的问题。另一种是间断的或跳跃的ox0xy如图：从直观上看，我们说一个函数在一点x=x0处连续是指这个函数的图象在x=x0处没有中断，所以以上图象就是连续函数的图象。也就是说，这个函数在点x0处是连续的。§2.6函数的连续性一、函数在某一点处的连续性)(.1xfy)()(lim)3()()(lim)(lim)2(.)1(000000xfxfxfxfxfxxxxxxx处有定义在2、11)(2xxxfoxy12.1处没有定义在x)1(1xx3、221)(xxxf11xx（1）在x=1处有定义5.2)(lim)2(1xfx2)(lim1xfx（3）函数f（x）的极限不存在。12oxy2.5yxo124、5.01)(xxf11xx（1）在x=1处有定义；（2）函数在x=1处的左右极限相等，即函数在x=1处的极限存在，且等于2，但不等于f（1）)1(5.02)(lim1fxfx导致函数图象断开的原因：1、函数在处没有定义1x2、函数在时极限不存在1x函数值不相等3、函数在处的极限值和1xoxy1212oxy2.5yxo12一般地，函数f（x）在点x0处连续必须同时具备三个条件：1、存在，即函数在点x0处有定义。)(0xf2、存在。)(lim0xfxx3、)()(lim00xfxfxx)(xfyxo12ox0xy)1()(lim1fxfx定义：设函数f(x)在处及其附近有定义，而且0xx)()(lim00xfxfxx则称函数f(x)在点处连续，0x称为函数f(x)的连续点。0x“连续必有极限，有极限未必连续”例1讨论下列函数在给定点处的连续性：.0,sin)()2(;0,1)()1(xxxhxxxf点点解：如图（1）函数在点x=0处没有定义，因而它在点x=0处不连续。xxf1)(（2）因为0sin0sinlim0xx.0sin)(处连续在点xxxh(3)f(x)=x+1(x≥0)X-1(x<0)在x=0处-1xy。10解：f(x)的定义域为：R,且)(lim0xfx1)(lim0xfx-1所以，)(lim0xfx不存在，从而f(x)在x=0处不连续。（4）f(x)=4723xx在x=2处，x=3处解：因为在x=2处，f(2)不存在，所以f(x)在x=2处不连续。在x=3处，f(3)=534从而，f(x)在x=3处连续。而lim3x3233)4lim()7lim(xxxx==5344723xx=f(3)注：判断函数在x=x0处的连续性有两法：)(xf（1）从图象上直观地判断；（2）从函数在x=x0处是否满足三个条件看)(xf二、单侧连续性：并且如果函数在点处及其右侧附近有定义0x)()(lim00xfxfxx则称f(x)在点处右连续。0x)(xfxyOa类似地：)()(lim00xfxfxx0x则称f(x)在处是左连续。如果函数在点x0处及其左侧附近有定义，并且)(xf221)(xxxf11xx12oxy2.5如例如函数),0(1),0(1)(xxxfxyo-11如图，在点x=0附近，),0(1)(lim0fxfx),0(1)(lim0fxfx因而函数在x=0处是右连续，而非左连续。)(xf结论：函数在一点处连续的充要条件是既左连续又右连续)(lim0xfxx)()(lim00xfxfxxox0xy)()(lim00xfxfxx三、函数的连续性：1、开区间内连续：如果在某一开区间内每一点处都连续，就说函数f（x）在开区间（a，b）内连续，或说f（x）是开区间（a，b）内的连续函数。)(xf),(ba2、闭区间上连续：如果函数在开区间内连续，在左端点处右连续，在右端点处左连续，就说函数在闭区间上连续。)(xf),(baaxbx)(xf],[ba例如，函数在闭区间[-1，1]上连续，而函数在开区间（0，1）内连续，在闭间[0，1]上不连续，因为它在左端点x=0处不是右连续。21xyxy11、连续函数的图象有什么特点？观察下列函数的图象，说出函数在x=a处是否连续：xyOaxyOaxyOaxyOaxyOaxyOa连续不连续连续不连续不连续不连续练习：（1）（2）（3）（4）（5）（6）axyo（7）不连续axyo（8）连续2、利用下列函数的图象，说明函数在给定点或开区间内是否连续。;0,1)()1(2xxxf点；xxxf0|,|)()2(点);,(,)()3(2开区间cbxaxxf).2,0(,24)()4(2开区间xxxf;0,1)()1(2xxxf点；xxxf0|,|)()2(点xyo);,(,)()3(2开区间cbxaxxf).2,0(,24)()4(2开区间xxxf不连续连续连续连续从几何直观上看，闭区间[a，b]上的一...