高二数学 空间向量的正交分解及其坐标表示课件 新人教版 课件VIP免费

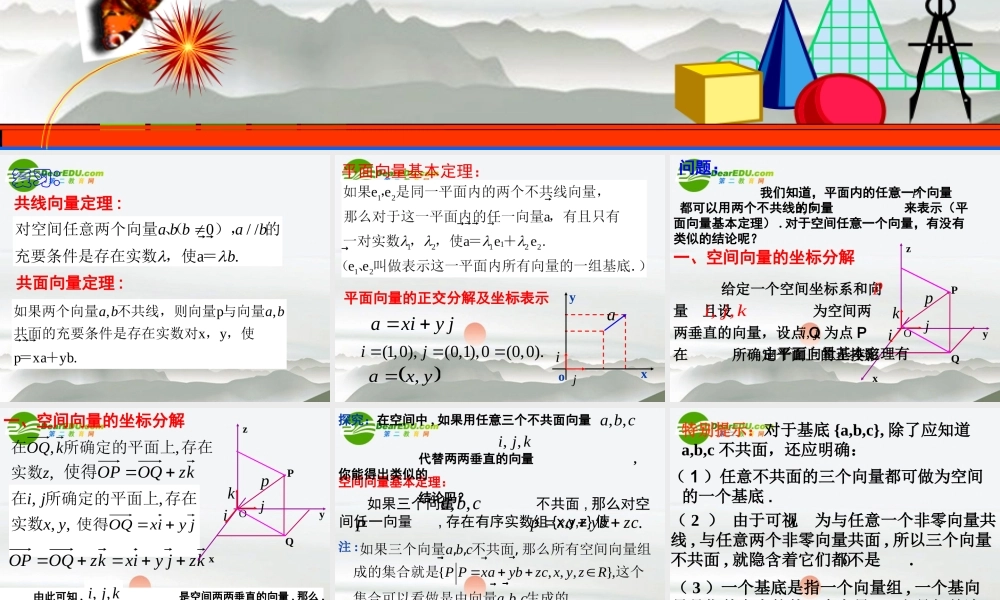
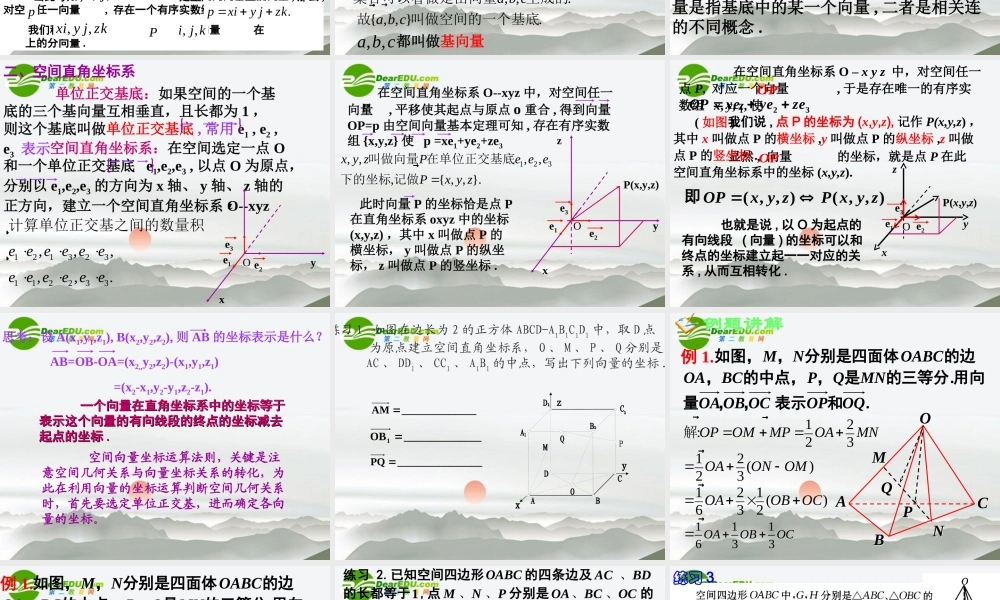
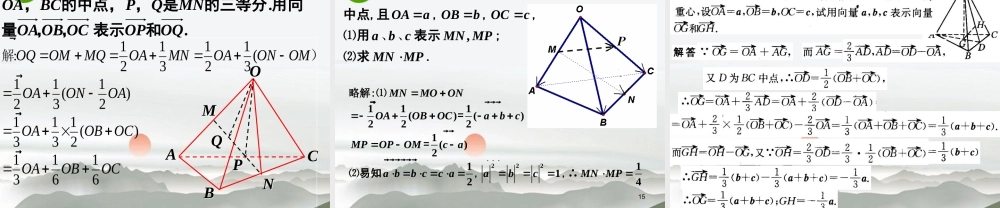
,p,xypxayb.a ba b如果两个向量不共线，则向量 与向量共面的充要条件是存在实数对 ， ，使＝＋共线向量定理 :复习：共面向量定理 :0/ /a.a b babb对空间任意两个向量 、（），的充要条件是存在实数 ，使 ＝平面向量基本定理：平面向量的正交分解及坐标表示xyoaijaxiy j(1,0),(0,1),0(0,0).ijyxa,问题： 我们知道，平面内的任意一个向量 都可以用两个不共线的向量 来表示（平面向量基本定理） . 对于空间任意一个向量，有没有类似的结论呢？,a bp�xyzOijkQPp�一、空间向量的坐标分解 给定一个空间坐标系和向量 且设 为空间两两垂直的向量，设点 Q 为点 P在 所确定平面上的正投影p�, ,i j k,i j由平面向量基本定理有一、空间向量的坐标分解,,,zkOQ实数存在所确定的平面上在,,, ,i jx y在所确定的平面上 存在实数jyixOQ使得kzOQOP使得kzjyixkzOQOPxyzQPp�Oijk 由此可知 , 如果 是空间两两垂直的向量 , 那么 ,对空间任一向量 , 存在一个有序实数组 {x,y,z} 使得 我们称 为向量 在 上的分向量 ., ,i j kP�.pxiy jzk�,,xi y j zk, ,i j kp�空间向量基本定理：都叫做基向量, ,a b c{, , ,},, ,. { , , }.a b cP Pxaybzc x y zRa b ca b c��������� 如果三个向量 , , 不共面, 那么所有空间向量组 成的集合就是这个 集合可以看做是由向量生成的故叫做空间的一个基底注 : 如果三个向量 不共面 , 那么对空间任一向量 , 存在有序实数组 {x,y,z} 使, ,a b cP�.pxaybzc�探究：在空间中 , 如果用任意三个不共面向量 代替两两垂直的向量 ,你能得出类似的 结论吗？, ,a b c�...