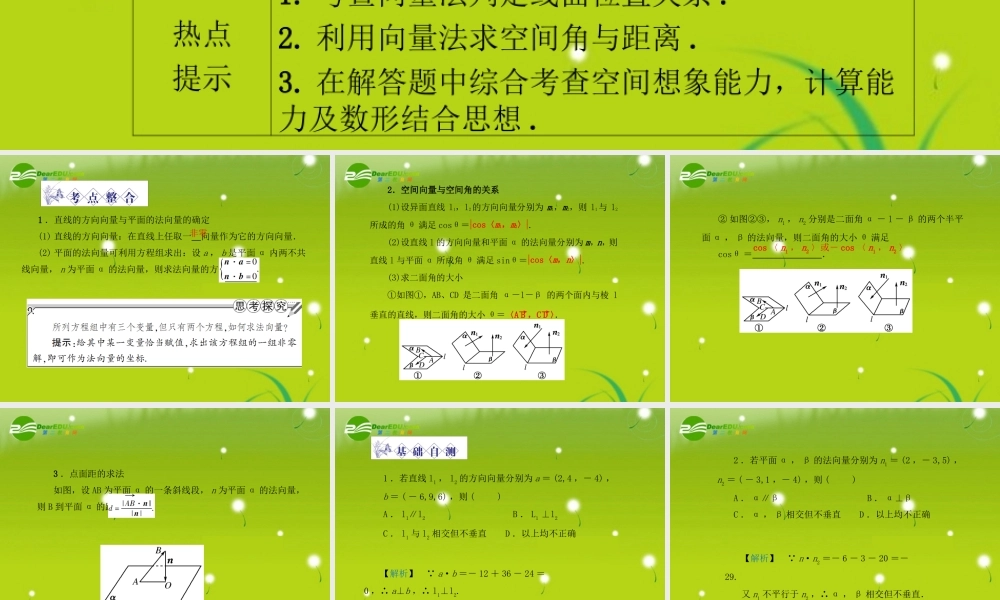
第八节立体几何中的向量方法考纲点击1. 理解直线的方向向量与平面的法向量 .2. 能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系 .3. 能用向量方法证明有关直线和平面位置关系的一些定理 ( 包括三垂线定理 ).4. 能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用 .热点提示1. 考查向量法判定线面位置关系 .2. 利用向量法求空间角与距离 .3. 在解答题中综合考查空间想象能力,计算能力及数形结合思想 .1 .直线的方向向量与平面的法向量的确定(1) 直线的方向向量:在直线上任取一 向量作为它的方向向量.(2) 平面的法向量可利用方程组求出:设 a , b 是平面 α 内两不共线向量, n 为平面 α 的法向量,则求法向量的方程组为非零2.空间向量与空间角的关系 (1)设异面直线 l1,l2的方向向量分别为 m1,m2,则 l1与 l2所成的角 θ 满足 cosθ=cos〈m1,m2〉 . (2)设直线 l 的方向向量和平面 α 的法向量分别为 m,n,则直线 l 与平面 α 所成角 θ 满足 sinθ=cos〈m,n〉 . (3)求二面角的大小 ①如图①,AB、CD 是二面角 α-l-β 的两个面内与棱 l垂直的直线,则二面角的大小 θ=〈A B→,C D→〉. ② 如图②③, n1 , n2 分别是二面角 α - l - β 的两个半平面 α , β 的法向量,则二面角的大小 θ 满足cosθ = .cos 〈 n1 , n2 〉或- cos 〈 n1 , n2 〉3 .点面距的求法如图,设 AB 为平面 α 的一条斜线段, n 为平面 α 的法向量,则 B 到平面 α 的距离1 .若直线 l1 , l2 的方向向量分别为 a = (2,4 ,- 4) ,b = ( - 6,9,6) ,则 ( )A . l1∥l2 B . L1 ⊥l2C . l1 与 l2 相交但不垂直D .以上均不正确【答案】 B【解析】 a·b =- 12 + 36 - 24 =0 ,∴ a⊥b ,∴ l1⊥l2.2 .若平面 α , β 的法向量分别为 n1 = (2 ,- 3,5) ,n2 = ( - 3,1 ,- 4) ,则 ( )A . α∥β B . α⊥βC . α , β 相交但不垂直D .以上均不正确【答案】 C【解析】 n·n2 =- 6 - 3 - 20 =-29.又 n1 不平行于 n2 ,∴ α , β 相交但不垂直.3 .若直线 l 的方向向量与平面 α 的法向量...