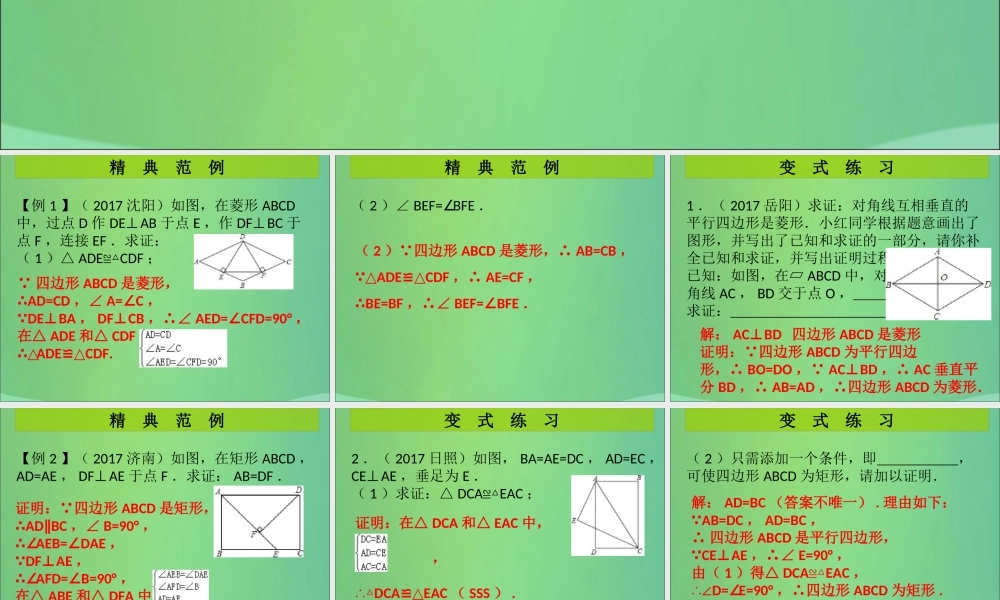
巩固提高精典范例(变式练习)中考热点加餐 菱形、矩形、正方形的性质与判定第一章 特殊的平行四边形【例 1 】( 2017 沈阳)如图,在菱形 ABCD中,过点 D 作 DE⊥AB 于点 E ,作 DF⊥BC 于点 F ,连接 EF .求证:( 1 )△ ADE≌△CDF ;精 典 范 例 四边形 ABCD 是菱形,∴AD=CD ,∠ A=C∠ , DEBA⊥, DFCB⊥,∴∠ AED=CFD=90°∠,在△ ADE 和△ CDF ,∴△ADECDF.≌△( 2 )∠ BEF=∠BFE .精 典 范 例( 2 ) 四边形 ABCD 是菱形,∴ AB=CB , △ADECDF≌△,∴ AE=CF ,∴BE=BF ,∴∠ BEF=BFE∠.1 .( 2017 岳阳)求证:对角线互相垂直的平行四边形是菱形.小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.已知:如图,在▱ ABCD 中,对角线 AC , BD 交于点 O , .求证: .变 式 练 习解: AC⊥BD 四边形 ABCD 是菱形证明: 四边形 ABCD 为平行四边形,∴ BO=DO , AC⊥BD ,∴ AC 垂直平分 BD ,∴ AB=AD ,∴四边形 ABCD 为菱形.【例 2 】( 2017 济南)如图,在矩形 ABCD ,AD=AE , DF⊥AE 于点 F .求证: AB=DF .精 典 范 例证明: 四边形 ABCD 是矩形,∴AD BC∥,∠ B=90° ,∴∠AEB=DAE∠, DFAE⊥,∴∠AFD=B=90°∠,在△ ABE 和△ DFA 中,∴△ABEDFA≌△,∴ AB=DF .2 .( 2017 日照)如图, BA=AE=DC , AD=EC ,CE⊥AE ,垂足为 E .( 1 )求证:△ DCA≌△EAC ;变 式 练 习证明:在△ DCA 和△ EAC 中, , ∴△DCAEAC≌△( SSS ) .( 2 )只需添加一个条件,即 ,可使四边形 ABCD 为矩形,请加以证明.变 式 练 习解: AD=BC (答案不唯一) . 理由如下: AB=DC , AD=BC ,∴ 四边形 ABCD 是平行四边形, CE⊥AE ,∴∠ E=90° ,由( 1 )得△ DCA≌△EAC ,∴∠D=∠E=90° ,∴四边形 ABCD 为矩形 .【例 3 】( 2017 广安)如图,四边形 ABCD是正方形, E , F 分别是 AB , AD 上的一点,且 BF⊥CE ,垂足为 G ,求证: AF=BE .精 典 范 例证明: 四边形 ABCD 是正方形,∴AB=BC ,∠ A=CBE=90°∠, BFCE⊥,∴∠ BCE+CBG=90°∠, ∠ABF+CBG=90°∠,∴∠BCE=ABF∠,在△ BCE 和△ ABF 中,,∴△BCEABF≌△( ...