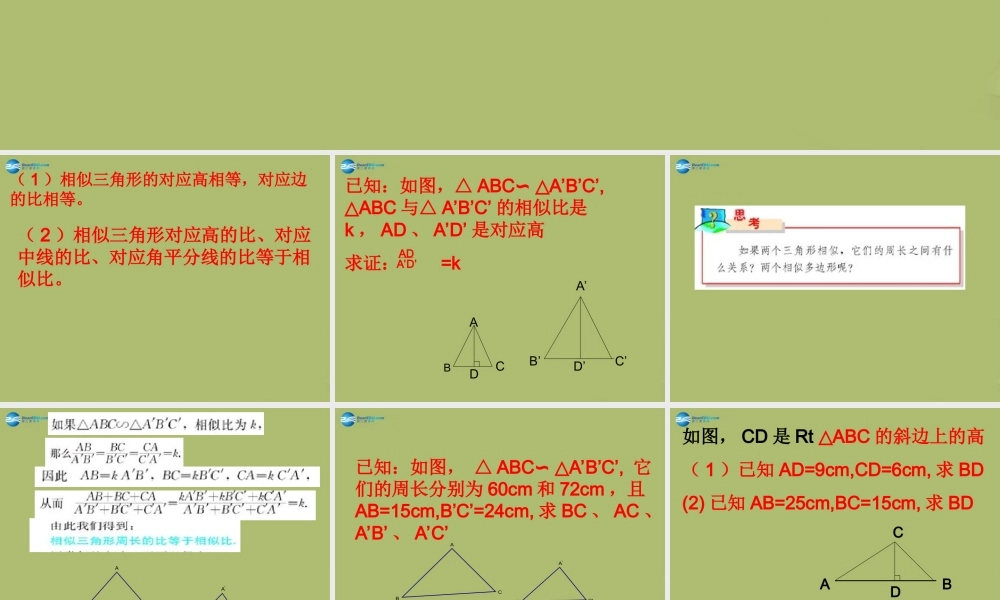
( 1 )相似三角形的对应高相等,对应边的比相等。( 2 )相似三角形对应高的比、对应中线的比、对应角平分线的比等于相似比。已知:如图,△ ABC A’B’C’, ∽ △ABC△与△ A’B’C’ 的相似比是k , AD 、 A’D’ 是对应高求证: =kADA’D’ABCDA’B’C’D’C'B'A'CBA已知:如图, △ ABC A’B’C’, ∽ △它们的周长分别为 60cm 和 72cm ,且AB=15cm,B’C’=24cm, 求 BC 、 AC 、A’B’ 、 A’C’C'B'A'CBA如图, CD 是 Rt ABC△的斜边上的高( 1 )已知 AD=9cm,CD=6cm, 求 BD(2) 已知 AB=25cm,BC=15cm, 求 BDABCD(4) 相似三角形的面积比等于相似比的平方• 如果两个相似三角形的面积之比为 1:9, 则它们对应边的比为 ;对应高的比为 。周长的比为 。• 如果两个相似三角形的面积之比为2:7, 较大三角形一边上的高为 ,则较小三角形对应边上的高为 。• 如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2 米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积为多少?FEDCBAL'LF'FBH例:如图,△ ABC 是一块锐角三角形余料,边BC=120 毫米,高 AD=80 毫米,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB 、 AC 上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形 PQMN 是符合要求的△ ABC 的高 AD 与 PN 相交于点 E 。设正方形 PQMN 的边长为 x 毫米。因为 PN BC∥,所以△ APN ABC∽ △所以AEAD=PNBC因此 ,得 x=48 (毫米)。答: ------- 。80–x80=x120