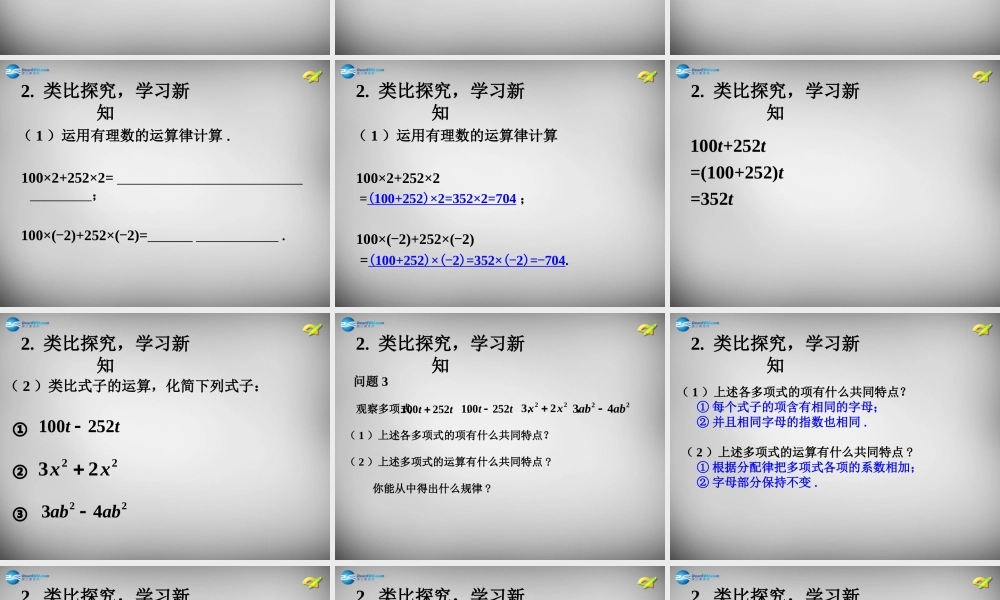
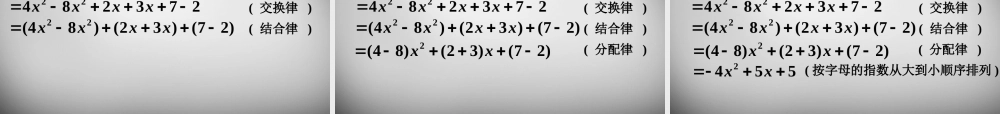2.2 2.2 整式的加减 整式的加减 (第(第 11 课时)课时) 本节课学习的主要内容是:同类项的概念、合并同类项的法则 . 整式的加减运算是“数与代数”领域中最基本的运算,它是今后学习整式的乘除、因式分解、分式、根式运算、方程及函数等知识的重要基础.同类项及合并同类项的法则是学习整式的加减运算和一元一次方程的直接基础.学习目标 :(1) 理解同类项的概念;(2) 掌握合并同类项的方法;(3) 通过类比数的运算探究合并同类项的法则,从 中体会数式通性和类比的数学思想. 学习重点:同类项的概念及合并同类项的法则,感受其中的“数式通性”和类比的数学思想.1. 创设情境,引入课题 问题 1 在西宁到拉萨路段,列车在冻土地段的行驶速度是 100 km/h ,在非冻土地段的行驶速度是 120 km/h ,列车通过非冻土地段所需时间是通过冻土地段所需时间的 2.1倍 ,如果通过冻土地段需要 t h ,你能用含t 的式子表示这段铁路的全长吗? 1. 创设情境,引入课题100t + 120×2.1t = 100t + 252t1. 创设情境,引入课题100t + 120×2.1t = 100t + 252t这个式子的结果是多少?你是怎样得到的 ?2. 类比探究,学习新知问题 2 整式的运算是建立在数的运算基础之上的,对于有理数的运算是怎样做的呢?整式的运算与有理数的运算有什么联系?2. 类比探究,学习新知( 1 )运用有理数的运算律计算 . 100×2+252×2= ; 100×(-2)+252×(-2)= .2. 类比探究,学习新知( 1 )运用有理数的运算律计算 100×2+252×2 =(100+252)×2=352×2=704 ; 100×(-2)+252×(-2) =(100+252)×(-2)=352×(-2)=-704.2. 类比探究,学习新知100t+252t=(100+252)t=352t2. 类比探究,学习新知( 2 )类比式子的运算,化简下列式子: ① ② ③2232xx100252tt2234abab2. 类比探究,学习新知 问题 3 观察多项式 , , , ( 1 )上述各多项式的项有什么共同特点? ( 2 )上述多项式的运算有什么共同特点 ? 你能从中得出什么规律 ? 2232xx100252tt2234abab100252tt2. 类比探究,学习新知 ( 1 )上述各多项式的项有什么共同特点? ① 每个式子的项含有相同的字母; ② 并且相同字母的指数也相同 . ( 2 )上述多项式的运算有什么共同特点 ? ① 根据分配律把多项式各项的系数相加; ② 字母部分保持不变 . 2. 类比探究,学习新知定义和法则:( 1 )所...