广东省高一数学正弦函数的图像和性质课件 北师大版 必修4 0 课件VIP免费

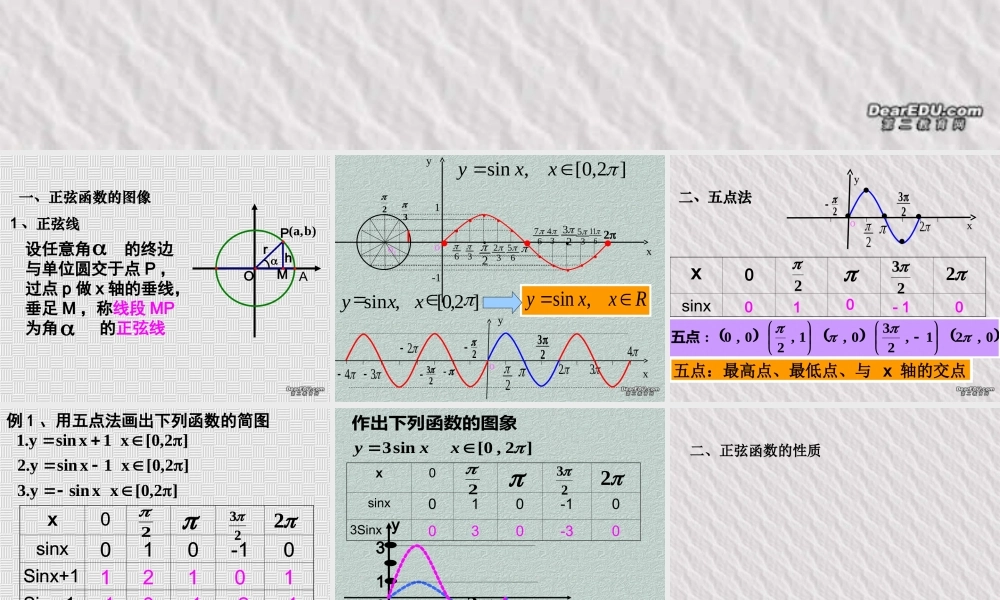
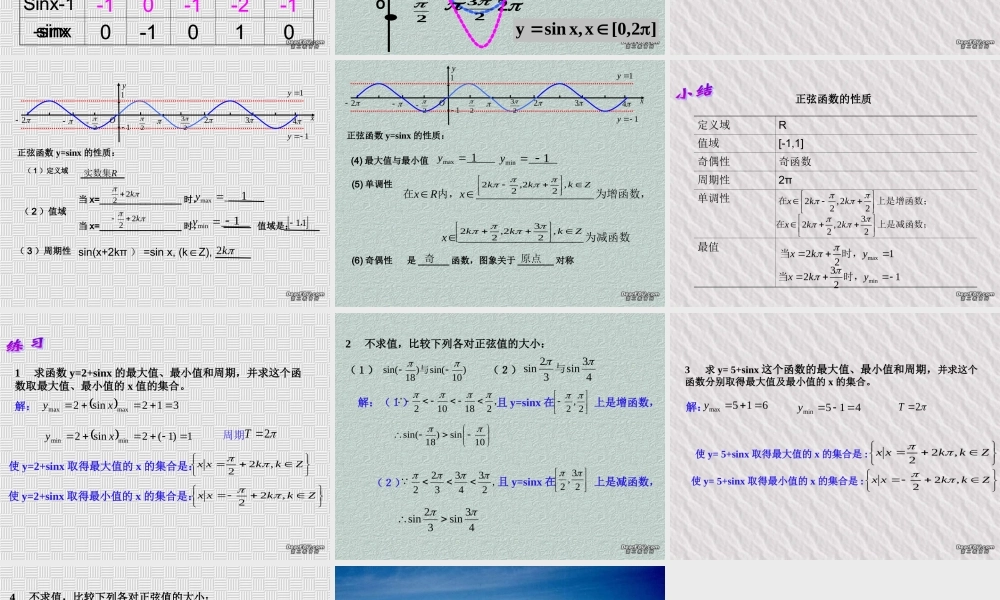
1.4-3 1.4-3 正弦正弦函数的图像和性质函数的图像和性质一、正弦函数的图像1 、正弦线rhOAPM)b,a(设任意角 的终边与单位圆交于点 P ，过点 p 做 x 轴的垂线，垂足 M ，称线段 MP为角 的正弦线·······6323265 ··· ·· ···236734356112yox]2,0[ ,sinxxyo11-1··322 232o34-2- 23423- yxRxxy ,sin]2,0[ ,sinxxy二、五点法0,21,230,1,20,0:五点2 232o2- yxxsinx22320- 10100五点：最高点、最低点、与 x 轴的交点例 1 、用五点法画出下列函数的简图]2,0[xxsiny.3]2,0[x1xsiny.2]2,0[x1xsiny.1x0sinx010-10Sinx+112101Sinx-1-10-1-2-1sinx0-10102232x0sinx010-10Sinx+112101Sinx-1-10-1-2-1-sinx0-10102232]2,0[sin3xxy作出下列函数的图象x0sinx010-103Sinx030-30223213oy2232]2,0[x,xsiny二、正弦函数的性质xOy11223222341y1y正弦函数 y=sinx 的性质：R实数集k22 1111，k2_____max y_____min ysin(x+2kπ ） =sin x, (kZ),∈（ 3 ）周期性当 x=________________ 时，当 x=________________ 时， 值域是： （ 2 ）值域 （ 1 ）定义域k22 (5) 单调性(6) 奇偶性是 ______ 函数，图象关于 _______ 对称为增函数，内，在_____________________xRx为减函数______________________x奇原点(4) 最大值与最小值_____max y_____min y11Zkkk,22,22Zkkk,232,22xOy11223222341y1y正弦函数 y=sinx 的性质：定义域R值域[-1,1]奇偶性奇函数周期性2π单调性最值正弦函数的性质2,222xkk在上是增函数；32,222xkk在上是减函数；max212xky当时，min3212xky当时，1 求函数 y=2+sinx 的最大值、最小值和周期，并求这个函数取最大值、最小值的 x 值的集合。解：使 y=2+sinx 取得最大值的 x 的集合是： Zkkxx,22使 y=2+sinx 取得最小值的 x 的集合是： ...