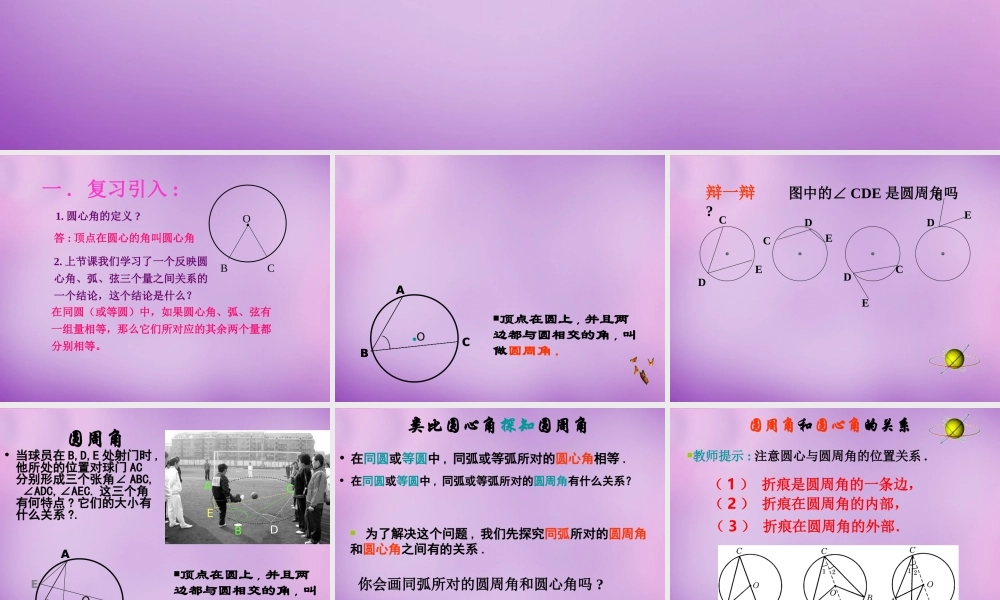
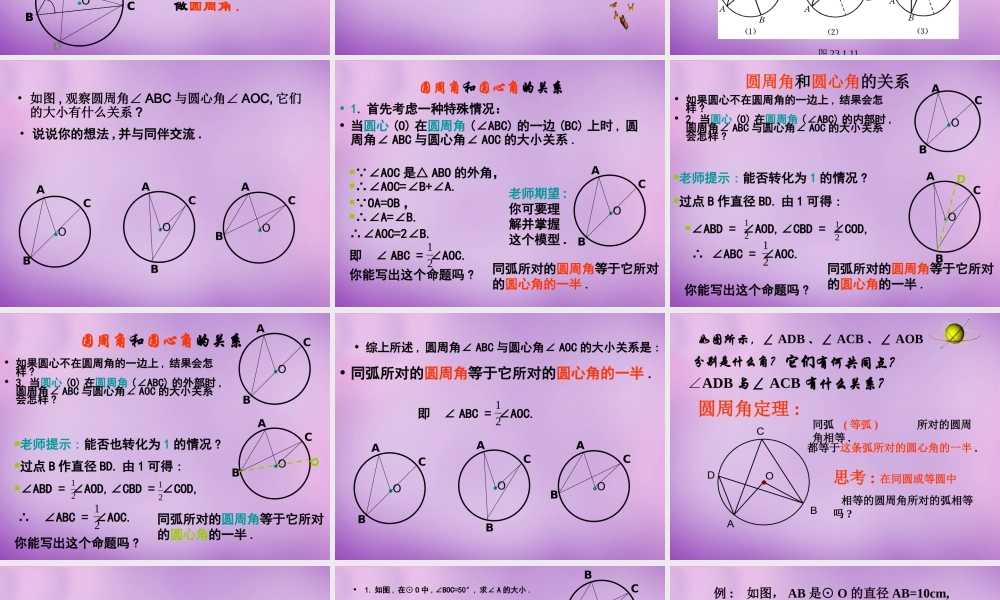
圆周角一 . 复习引入 :1. 圆心角的定义 ?.OBC在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。答 : 顶点在圆心的角叫圆心角2. 上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?顶点在圆上 , 并且两边都与圆相交的角 , 叫做圆周角 .●OBACBACBACBACBACBAC辩一辩 图中的∠ CDE 是圆周角吗? CDECDECDECDE圆周角• 当球员在 B,D,E 处射门时 ,他所处的位置对球门 AC分别形成三个张角∠ ABC, ∠ADC,∠AEC. 这三个角有何特点 ? 它们的大小有什么关系 ?.●OBACBACBACBACBACBACBACDEDE顶点在圆上 , 并且两边都与圆相交的角 , 叫做圆周角 .类比圆心角探知圆周角• 在同圆或等圆中 , 同弧或等弧所对的圆心角相等 .• 在同圆或等圆中 , 同弧或等弧所对的圆周角有什么关系? 为了解决这个问题 , 我们先探究同弧所对的圆周角和圆心角之间有的关系 .你会画同弧所对的圆周角和圆心角吗 ?圆周角和圆心角的关系教师提示 : 注意圆心与圆周角的位置关系 . 图 23.1.11 ( 1 ) 折痕是圆周角的一条边, ( 2 ) 折痕在圆周角的内部, ( 3 ) 折痕在圆周角的外部. • 如图 , 观察圆周角∠ ABC 与圆心角∠ AOC, 它们的大小有什么关系 ?• 说说你的想法 , 并与同伴交流 .●OABC●OABC●OABC圆周角和圆心角的关系• 1. 首先考虑一种特殊情况:• 当圆心 (O) 在圆周角 (∠ABC) 的一边 (BC) 上时 , 圆周角∠ ABC 与圆心角∠ AOC 的大小关系 . ∠AOC 是△ ABO 的外角,∴∠AOC=∠B+∠A. OA=OB ,●OABC∴∠A=∠B.∴∠AOC=2∠B.即 ∠ ABC = ∠AOC.21你能写出这个命题吗 ?同弧所对的圆周角等于它所对的圆心角的一半 .老师期望 :你可要理解并掌握这个模型 .• 如果圆心不在圆周角的一边上 , 结果会怎样 ?• 2. 当圆心 (O) 在圆周角 (∠ABC) 的内部时 ,圆周角∠ ABC 与圆心角∠ AOC 的大小关系会怎样 ?老师提示 : 能否转化为 1 的情况 ?过点 B 作直径 BD. 由 1 可得 :●O ∴ ∠ABC = ∠AOC.21你能写出这个命题吗 ?同弧所对的圆周角等于它所对的圆心角的一半 .ABCD∠ABD = ∠AOD,∠CBD = ∠COD,2121圆周角和圆心角的关系●OABC圆周角和圆心角的关系• 如果圆心不在圆周角的一边上 , 结果会怎样 ?• 3. 当圆心 (O)...